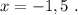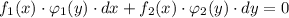
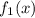 и
и 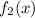 зависят только от переменной "х" , а функции
зависят только от переменной "х" , а функции 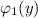 и
и 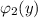 зависят только от переменной "у" . Указывается на то, что диффер. уравнение допускает обособление (разделение) переменных только тогда, когда перед дифференциалами (dx и dy) стоят функции, являющиеся произведениями двух других функций, одна из которых зависит только от "х" , а вторая зависит только от "у" .
зависят только от переменной "у" . Указывается на то, что диффер. уравнение допускает обособление (разделение) переменных только тогда, когда перед дифференциалами (dx и dy) стоят функции, являющиеся произведениями двух других функций, одна из которых зависит только от "х" , а вторая зависит только от "у" . 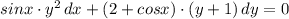 .
. 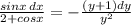 .
.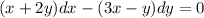 , то переменные уже нельзя разделить, так как нельзя функции, стоящие перед dx и dy,представить в виде произведения
, то переменные уже нельзя разделить, так как нельзя функции, стоящие перед dx и dy,представить в виде произведения 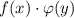 .
.
ответ: а=4 .
Для того , чтобы значение функции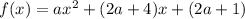 было меньше или равно 0 только для одного значения "х", необходимо, чтобы парабола y=f(x) имела только одну общую точку с осью ОХ (у=0) и чтобы ветви параболы были направлены вверх (a>0). Тогда будет выполняться система
было меньше или равно 0 только для одного значения "х", необходимо, чтобы парабола y=f(x) имела только одну общую точку с осью ОХ (у=0) и чтобы ветви параболы были направлены вверх (a>0). Тогда будет выполняться система
ответ: а=4 .
Действительно, при а=4 получаем неравенство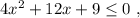
Но квадрат любого выражения больше или равен 0, поэтому из неравенства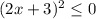 можно выбрать только знак "=" , а
можно выбрать только знак "=" , а 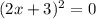 только при одном значении
только при одном значении