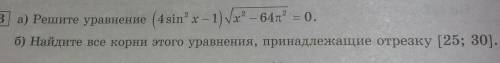
Нам нужно найти при каких значениях а уравнение (а + 4)х = а - 3 не имеет корней.
Давайте сначала выразим из уравнения переменную х через а.
Разделим обе части уравнения на скобку (а + 4):
х = (а - 3)/(а + 4).
Рассмотрим полученное равенство.
В выражении стоящем в правой части равенства есть знак дроби ( иными словами деления).
Нам известно, что на ноль делить нельзя. Найдя те значения а которые обращают знаменатель в ноль и будут ответом на вопрос задания.
а + 4 = 0;
а = - 4.
При а = - 4 знаменатель дроби обращается в 0, следовательно уравнение не имеет корней.
ответ: б = -4.
Пусть х пельменей в час - производительность Валентины, тогда (х + 2) пельменя в час - производительность Софьи. На лепку 112 пельменей Валентина затрачивает на 8 часов меньше, чем Софья на лепку 360 таких же пельменей. Уравнение:
360/(х+2) - 112/х = 8
360 · х - 112 · (х + 2) = 8 · х · (х + 2)
360х - 112х - 224 = 8х² + 16х
8х² + 16х - 360х + 112х + 224 = 0
8х² - 232х + 224 = 0
Разделим обе части уравнения на 8
х² - 29х + 28 = 0
D = b² - 4ac = (-29)² - 4 · 1 · 28 = 841 - 112 = 729
√D = √729 = 27
х = (-b±√D)/(2a)
х₁ = (29-27)/(2·1) = 2/2 = 1 (не подходит по условию задачи)
х₂ = (29+27)/(2·1) = 56/2 = 28
ответ: 28 пельменей в час лепит Валентина.
Проверка:
112 : 28 = 4 ч - время работы Валентины
360 : (28+2) = 360 : 30 = 12 ч - время работы Софьи
12 ч - 4 ч = 8 ч - разница
8П; 49П/6; 53П/6; 55П/6
Объяснение:
Найти корни на отрезке [25; 30] ≈ [7,96П; 9,55П]
И в скобках, и под корнем - разности квадратов. Раскладываем.
Теперь можно приравнять к 0 каждую из скобок.
1) 2sin x - 1 = 0
sin x = 1/2
x = П/6 + 2Пk
В отрезок [7,96П; 9,55П] попадает корень:
x1 = П/6 + 8П = 49П/6 ≈ 8,17П
x = 5П/6 + 2Пk
В отрезок [7,96П; 9,55П] попадает корень:
x2 = 5П/6 + 8П = 53П/6 ≈ 8,83П
2) 2sin x + 1 = 0
sin x = -1/2
x = -П/6 + 2Пk
Пробуем подобрать корни
x = -П/6 + 8П ≈ -0,17П + 8П = 7,83П < 7,96П
x = -П/6 + 10П ≈ -0,17П + 10П = 9,83П > 9,55П
В отрезок [7,96П; 9,55П] не попадает ни один корень.
x = -5П/6 + 2Пk
В отрезок [7,96П; 9,55П] попадает корень:
x3 = -5П/6 + 10П = 55П/6 ≈ 9,17П
3) x - 8П = 0
x4 = 8П - попадает в отрезок [7,96П; 9,55П].
4) x + 8П = 0
x = 8П - не попадает в отрезок [7,96П; 9,55П].