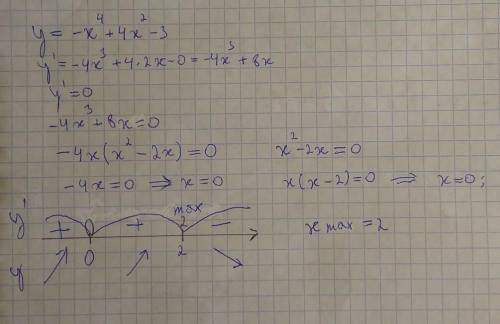
![y=-x^4+4x^2-3\\\\y'=-4x^3+8x=-4x\, (x^2-2)=-4x\, (x-\sqrt2)(x+\sqrt2)=0\\\\x_1=0\ ,\ \ x_2=-\sqrt2\ ,\ \ x_3=\sqrt2\\\\znaki\ y'(x):\ \ \ ---(-\sqrt2)+++(0)---(\sqrt2)+++\\\\{}\qquad \qquad \qquad \quad \ \searrow \ \ (-\sqrt2)\ \ \nearrow\ \ \ (0)\ \ \ \searrow \ \ \ (\sqrt2)\ \ \ \nearrow \\\\\\y(x)\ vozrastaet:\ \ x\in [-\sqrt2\, ;\, 0\, ]\cup [\, \sqrt2\, ;+\infty )\\\\y(x)\ ybuvaet:\ \ x\in (-\infty\, ;-\sqrt2\ ]\cup [\ 0\, ;\sqrt2\ ]](/tpl/images/1356/2736/b4c26.png)
у=1
Объяснение:
берем x-y=2 и выносим у в правую часть и получаем : x=2+y . Из этого мы уже получаем одно уравнение и вместо x подставляем это значение в 1 уравнение. 2*(2+у)-3у=3 и решаем его . 1 действие (это раскрываем скобки) - 4+2у-3у=3 . 2 действие (это все что можно сложить складываем) - 4-у=3. 3 действие ( это 4 переносим в правую сторону , но при этом не забываем что когда переносим в какую либо сторону не зависимо в правую или левую , то переносим с противоположным знаком) получаем : -у = -4+3. -у= -1 . 4 действие ( это -y так оставить нельзя и чтобы его убрать мы в правую часть умножаем еще на -1 и в правой части минус на минус дает плюс и получаем положительное число ) : y=1
Условию удовлетворяет только одна пятерка последовательных натуральных чисел:
10; 11; 12; 13; 14
и
10²+11²+12² = 13²+14² = 365
Объяснение:
Пусть, x - первое число последовательности.
Т.к. нам нужны пять последовательных натуральных (то есть целых, неотрицательных) чисел, то они будут выглядеть так:
x; x+1; x+2; x+3; x+4
Причем x > 0
Известно, что равны:
- сумма квадратов первых трёх чисел
- сумма квадратов двух последних чисел.
т е.
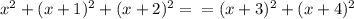
Преобразуем, раскрыв скобки:

По Т. Виетта:
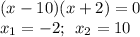
или через дискр-нт. Т.к. b четное, возьмем D/4:
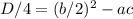
а корни будут равны
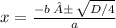
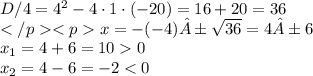
Так как в условии указано, что числа - последовательные натуральные, значение
x= -2 - не подходит, т.к. число -2 отрицательное и не является натуральным
Следовательно, первое число из пяти искомых - это 10, а вся последовательность имеет вид:
10; 11; 12; 13; 14
Проверим - и действительно:
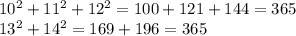
сумма квадратов первых трёх чисел равна сумме квадратов двух последних чисел.