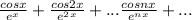
1) f(-3,5) = -0.5; f(-2,5) = 2; f(-1) = 0; f(2) = -1.
Здесь последовательно находим абсциссы х=-0,5; х=-2,5; х=-1; х=2, проводим прямую, параллельно оси оу до точки пересечения с графиком и называем, чему в этой точке равна ордината.
2) f(x)=-2,5, если х = 5 ; f(x)=-2, если х=3,5;
f(x)=0, если х=-3, х=-1, х=1,5;
f(x)=2, если х=0; х=-1,5, х=-2,5.
Здесь наоборот, по известной ординате, у=-2,5; у=-2; у=0; у=2 находим абсциссу х, их может быть несколько, т.к. прямая, параллельная оси ох пересекает график в нескольких точках, опускаем из этих точек перпендикуляры на ось ох и читаем ответы
3) Е(у) = [-2,5; 3]- это те значения, которые пробегает у. самое маленькое у=-2,5, самое большое у=3.
Необходимое условие сходимости выполняется только при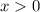
Поскольку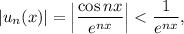 а при
а при 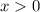 ряд
ряд 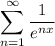 сходится по радикальному признаку Коши:
сходится по радикальному признаку Коши:
то заданный ряд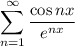 сходится по признаку сравнения при
сходится по признаку сравнения при 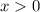
Таким образом, область сходимости заданного ряда: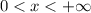
ответ: