


0,5+m
Объяснение:
Для того, чтобы найти требуемое значение логарифма log49(28), которого обозначим через L, воспользуемся следующей формулой loga(b / с) = logab / logaс (где а > 0, a ≠ 1, b > 0, c > 0), которая называется формулой перехода к новому основанию.
В нашем примере новым основанием будет число 7, так как дано log7(2) = m. Итак, имеем L = log7(28) / log7(49). Поскольку 28 = 7 * 22 и 49 = 72, то используя следующие формулы, преобразуем полученное выражение: loga(b * с) = logab + logaс (где а > 0, a ≠ 1, b > 0, c > 0) и logabn = n * logab (где а > 0, a ≠ 1, b > 0, n – любое число). Получим: L = log7(7 * 22) / log7(72) = (log7(7) + log7(22)) / log7(72) = (log7(7) + 2 * log7(2)) / (2 * log7(7)).
Очевидно, что log7(7) = 1. Тогда, имеем: L = (1 + 2 * m) / (2 * 1) = 1 : 2 + 2 * m : 2 = 0,5 + m.
Объяснение:
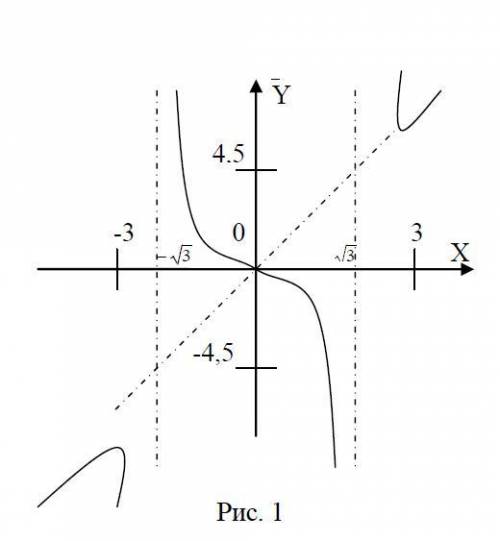
График и исследование по вложении