Question

Сформулируйте и докажите теорему выражающую первый признак подобия треугольников

Answer 1

Теорема. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники являются подобными

Доказательство:

Пусть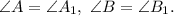 $\angle A=\angle A_1,~\angle B=\angle B_1.$ Так как сумма углов треугольника равна 180°, то для треугольников ABC и A₁B₁C₁ можем записать равенства:

$\angle A+\angle B+\angle C=180а,~~~~ \angle A_1+\angle B_1+\angle C_1=180а$

Выражаем из первого равенства угол С, а из второго равенства угол C₁, получим :

$\angle C=180а-\angle A-\angle B,~~~ \angle C_1=180а-\angle A_1-\angle B_1$, тогда $\angle C=\angle C_1$, то есть у треугольников ABC и A₁B₁C₁ углы соответственно равны.

Если угол одного треугольника равен углу другого треугольника, то площади треугольников относятся как произведение сторон, заключающих равные углы.

То есть,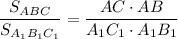 $\displaystyle \frac{S_{ABC}}{S_{A_1B_1C_1}} =\dfrac{AC\cdot AB}{A_1C_1\cdot A_1B_1}$ - для $\angle A=\angle A_1$

Так как $\angle C=\angle C_1$, то $\displaystyle \frac{S_{ABC}}{S_{A_1B_1C_1}} =\frac{CB\cdot CA}{C_1B_1\cdot C_1A_1}$

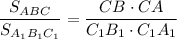
Приравнивая, получим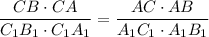 $\displaystyle \frac{CB\cdot CA}{C_1B_1\cdot C_1A_1} =\frac{AC\cdot AB}{A_1C_1\cdot A_1B_1}$, получим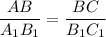 $\displaystyle \frac{AB}{A_1B_1}=\frac{BC}{B_1C_1}$

Аналогично для ∠A = ∠A₁ и ∠B = ∠B₁, имеет место равенство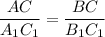 $\displaystyle \frac{AC}{A_1C_1}=\frac{BC}{B_1C_1}$

Следовательно,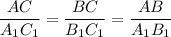 $\dfrac{AC}{A_1C_1}=\dfrac{BC}{B_1C_1} =\dfrac{AB}{A_1B_1}$, то есть получили что стороны треугольников пропорциональны.