Question

Профильный уровень с заданием.

Answer 1

4

Объяснение:

sinх>cos2x  .

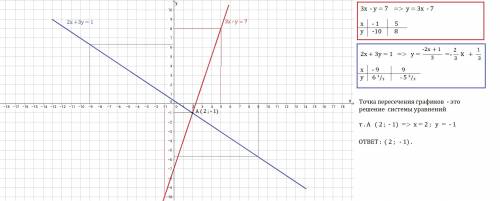
Построим два графика на  0≤х≤2π  . Найдем значения на оси ох , где график у=sinх выше графика у=cos2x  . Это отрезок от 5π\6 до π\6. Длина этого отрезка  5π\6 - π\6=4π\6=2π\3

По условию (6*2п\3): π=4.

-----------------------------

Некоторые вычисления :

---------------------------

у=sinх  ,синусоида , достигает максимального значения 1 в π\2,

минимального значения -1 в 3π\2.

Пересекает ось ох при х=0, π, 2π

---------------------------------

у=cos2x косинусоида сжатая в 2 раза , достигает максимального значения 1 в 0,  минимального значения -1 в π\2.

Пересекает ось ох при х=π\4,  3π\4

------------------------------

Найдем точки пересечения , обозначенные на графике

sinх=cos2x  . sinх=1-sin²х  , 2sin²х+sinх-1=0  ,

sinх=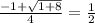$\frac{-1+\sqrt{1+8} }{4} =\frac{1}{2}$  ,   на  0≤х≤2π  ,  х=5π\6 , х= π\6.

sinх=$\frac{-1-\sqrt{1+8} }{4} =-1$  , на  0≤х≤2π ,  х=3π\2 .

--------------------------------