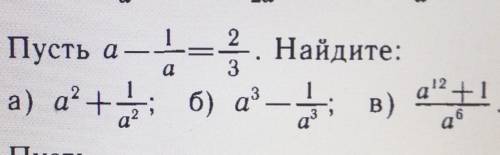
На фото
Объяснение:


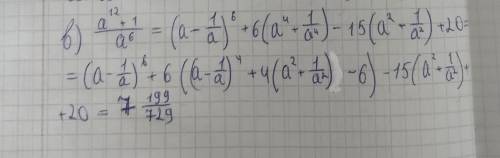
1) 2sin²x+11sinx+5=0
sinx=t
2t²+11t+5=0
D=121-40=81; 9
t=-11±9/4
t1=-5, t2=-0.5
2) 2sin²x-3sinx-2=0
sinx=t
2t²-3t-2=0
D=9+16=25; 5
t=3±5/4;
t1=-0.5, t2=2
3) 2sin²-7sinx-4=0
sinx=t
2t²-7t-4=0
D=49+32=81; 9
t=7±9/4
t1=-0.5, t2=4
4) 2cos²x+7cosx-4=0
cosx=t
2t²+7t-4=0
D=49+32=81; 9
t=-7±9/4
t1=-4, t2=0.5
5) -8cos²x+4=0
cos²x=t
-8t+4=0
-8t=-4
t=0.5
6) 2cos²x+3cosx-2=0
cosx=t
2t²+3t-2=0
D=9+16=25; 5
t=-3±5/4
t1=-0.5, t2=2
7) 4sin²x+12sinx+5=0
sinx=t
4t²+12t+5=0
D=144-80=64; 8
t=-12±8/8
t1=0.5, t2=1.5
8) 4cos²x+12cosx+5=0
cosx=t
4t²+12t+5=0
D=144-80=64; 8
t=-12±8/8
t1=0.5, t2=1.5
а)а-(1/а)=2/3⇒а²+(1/а²)-2а/а=4/9⇒а²+(1/а²)=2 4/9=22/9
б) а³-(1/а³)=(а-(1/а))(а²+1+(1/а²))=(2/3)*(1+2 4/9)=2*31/(3*9)=62/27=2 8/27
в)(а¹²+1)/а⁶=а⁶+(1/а⁶)=(а²)³+(1/а²)³=(а²+(1/а²))*(а⁴+(1/а⁴)-1)=
(22/9)*((а²+(1/а²))²-3)=22/9*((22/9)²-3)=22*(484-243)/(81*9)=22*241/729=
5302/729=7 199/729