Света раскладывала конфеты в вазочки, в первую вазочку света положила половину от всех конфет и ещё пол конфеты.В каждой последующей вазочке Света оставляла половину из оставшихся конфет и ещё пол конфеты. Всего было 7 вазочек, сколько было конфет
Пусть конфет было . Разложение в 7 вазочек половины конфет, половины от половины и т. д., а также полконфеты рассмотрим как геометрическую прогрессию с первым членом и знаменателем , Рассмотрим сумму данной прогрессии (по условию эта сумма равна количеству конфет, то есть ):
1а) Каждая монета может упасть либо орлом (О) либо решкой (Р), то есть две возможности.Монет всего 3.Тогда число возможных событий для 3-х монет равно 2^3=8.Вот варианты: (РРР) (РРО) (РОР) (ОРР) (ООР) (ОРО) (РОО) (ООО) Два раза орёл и один раз решка выпадает в трёх случаях (ООР) (ОРО) (РОО). Вероятность равна 3/8. 1б) Если монету бросают дважды, то возможны случаи (ОО) (ОР) (РО) (РР) Вероятность ХОТЯ бы один раз выпасть орлу равна 3/4. 2) Двойка выпадает с вероятностью 1/6 и пятёрка выпадает с вероятностью 1/6 . Вероятность того, что выпадет или 2 или 5 равна 1/6+1/6=2/6=1/3 б)Чисел, меньших 3, на кубике всего два.Чисел,не больших 3 (меньше или равно 3),на кубике всего 3.Вероятность события равна 2/6*3/6=6/36=1/6
1а) Каждая монета может упасть либо орлом (О) либо решкой (Р), то есть две возможности.Монет всего 3.Тогда число возможных событий для 3-х монет равно 2^3=8.Вот варианты: (РРР) (РРО) (РОР) (ОРР) (ООР) (ОРО) (РОО) (ООО) Два раза орёл и один раз решка выпадает в трёх случаях (ООР) (ОРО) (РОО). Вероятность равна 3/8. 1б) Если монету бросают дважды, то возможны случаи (ОО) (ОР) (РО) (РР) Вероятность ХОТЯ бы один раз выпасть орлу равна 3/4. 2) Двойка выпадает с вероятностью 1/6 и пятёрка выпадает с вероятностью 1/6 . Вероятность того, что выпадет или 2 или 5 равна 1/6+1/6=2/6=1/3 б)Чисел, меньших 3, на кубике всего два.Чисел,не больших 3 (меньше или равно 3),на кубике всего 3.Вероятность события равна 2/6*3/6=6/36=1/6
Пусть конфет было . Разложение в 7 вазочек половины конфет, половины от половины и т. д., а также полконфеты рассмотрим как геометрическую прогрессию с первым членом
. Разложение в 7 вазочек половины конфет, половины от половины и т. д., а также полконфеты рассмотрим как геометрическую прогрессию с первым членом 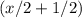 и знаменателем
и знаменателем 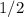 , Рассмотрим сумму данной прогрессии (по условию эта сумма равна количеству конфет, то есть
, Рассмотрим сумму данной прогрессии (по условию эта сумма равна количеству конфет, то есть  ):
):
ответ: 127 шт.