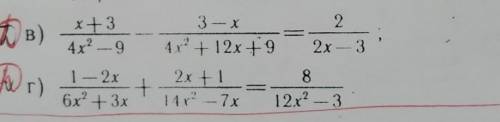
Объяснение:
в) (x + 3)/*((2x - 3)(2x + 3)) - (3 - x)/((2x + 3)^2) - 2/(2x - 3) = 0
(2x ^2 + 3x + 6x + 9 - 6x + 2x^2 + 9 - 3x - 8x^2 - 24x - 18)/((2x - 3)(2x + 3)^2) =
= (- 4x^2 - 24x)/((2x - 3)(2x + 3)^2)
Уравнение равно нулю, если числитель равен нулю
- 4x^2 - 24x = 0 |: (-4)
x^2 + 6x = 0
x(x + 6) = 0
x = 0
x = - 6
г) ОДЗ 2x ± 1 ≠ 0
x ≠ ± 0,5
x ≠ 0
(1 - 2x)/(3x(2x + 1)) + (2x + 1)/(7x(2x - 1)) - 8/(3(2x - 1)(2x + 1)) = 0
(14x - 28x^2 - 7 + 14x + 12x^2 + 6x +6x + 3 - 56x)/(21x(2x - 1)(2x + 1)) =
= (-16x^2 - 16x - 4)/(21x(2x - 1)(2x + 1))
Уравнение равно нулю, если числитель равен нулю
-16x^2 - 16x - 4 = 0 | : (-4)
4x^2 + 4x + 1 = 0
(2x + 1)^2 = 0
x = -0,5 - ∅ (ОДЗ)
ответ - решения нет
Объяснение:
☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆