
(-3;-17) - точка экстремума функции (минимум)
Объяснение:
Точки экстремума - это такие точки, в которых значение функция, скажем так, меняет свою скорость роста. То есть до неё функция либо возрастала, либо убывала, а после неё наоборот - начинает либо убывать, либо возрастать.
Для нахождения точки экстремума потребуется найти производную 1 порядка:
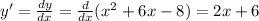
После этого мы приравниваем получившуюся функцию к нулю и решаем получившееся уравнение:
2x+6=0 => 2x=-6 => x=-3
но необходимо убедиться, что данная точка действительно является экстремумом, для этого мы смотрим как ведёт себя функция y' до и после точки x0=-3 (можно подставить любые значения <-3 а потом значение >-3, если получаются разные по знаку числа, к примеру отрицательное-положительное или положительное-отрицательное, то данная точка действительно является экстремумом функции y, а точнее в данном случае она является минимумом).
Ну а теперь осталось подставить значение x0=-3 в изначальную функцию y и найти y0
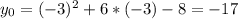
Ну и запишем ответ:
(-3;-17) - точка экстремума функции (а точнее - минимум)
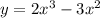
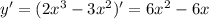
Необходимые условия экстремума:
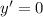
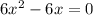
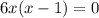

Имеем две критические (стационарные) точки:  и
и 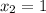
Достаточные условия экстремума: если при переходе через критическую точку производная непрерывной функции меняет знак на противоположный, то имеем экстремум функции в этой точке.
Если точка с абсциссой  меняет знак с "+" на "–" (двигаясь в направлении увеличения
меняет знак с "+" на "–" (двигаясь в направлении увеличения  ), то
), то  — точка максимума, а если с "–" на "+" , то
— точка максимума, а если с "–" на "+" , то  — точка минимума.
— точка минимума.
Из промежутка 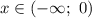 выберем, например,
выберем, например,  и имеем:
и имеем: 
Из промежутка 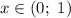 выберем, например,
выберем, например, 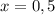 и имеем:
и имеем: 
Имеем максимум в точке с абсциссой 
Из промежутка 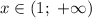 выберем, например,
выберем, например, 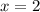 и имеем:
и имеем: 
Имеем минимум в точке с абсциссой 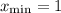
ответ: 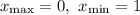
Данное неравенство равносильно системе неравенств:
Нули модулей:
Раскроем модули на пяти участках, используя правило раскрытия модуля:
Учитывая условие,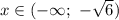
Учитывая условие,![x \in [-\sqrt{6}; \ -2]](/tpl/images/1358/0885/b61eb.png)
Учитывая условие,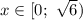
Учитывая условие,![x \in [\sqrt{6}; \ 3]](/tpl/images/1358/0885/fab66.png)
Нет решений.
Объединим все пять случаев решения:
Имеем:
Находим пересечение решений:
Ограничения:
Учитывая условие,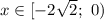
Объединяем решения:
Получили решения обоих неравенств в системе неравенств:
Находим пересечение решений:
ответ:![x \in [-2\sqrt{2}; \ -2] \cup (0; \ 2)](/tpl/images/1358/0885/8c02c.png)