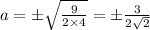Максимальность разности корней уравнения эквивалента максимальности квадрата разности этих корней. Пусть у вышеприведенного уравнения корни . Требуется определить максимальное значение : .
Для первой задачи . Нужно максимизировать . Это парабола в системе координат , если сделать замену . Таким образом, максимум достигается при
Привет! Я с удовольствием выступлю в роли школьного учителя и помогу тебе разобраться с данной задачей.
Итак, у нас есть конкурс «Художественное слово», где участники выступают и оцениваются по трём параметрам: артистизм, актуальность поднятой темы и уровень соответствия авторскому тексту. Каждый параметр имеет начальную оценку, которую можно получить просто за наличие этого параметра в выступлении.
Далее, пять независимых судей ставят оценки по каждому параметру, от 1 до 4. Однако, чтобы обеспечить объективность, самая высокая оценка отбрасывается.
Теперь нужно высчитать итоговую оценку, которая будет суммой начальной оценки и средней арифметической оставшихся оценок.
Давай разберемся на примере. Предположим, начальные оценки за каждый параметр такие:
Артистизм - 3
Актуальность поднятой темы - 2
Уровень соответствия авторскому тексту - 4
Максимальность разности корней уравнения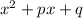 эквивалента максимальности квадрата разности этих корней. Пусть у вышеприведенного уравнения корни
эквивалента максимальности квадрата разности этих корней. Пусть у вышеприведенного уравнения корни 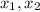 . Требуется определить максимальное значение
. Требуется определить максимальное значение 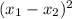 :
: 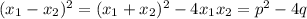 .
.
Для первой задачи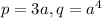 . Нужно максимизировать
. Нужно максимизировать 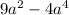 . Это парабола в системе координат
. Это парабола в системе координат 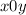 , если сделать замену
, если сделать замену 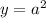 . Таким образом, максимум достигается при
. Таким образом, максимум достигается при