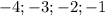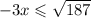
- 1; - 2; - 3; - 4 .
Объяснение:
- 3х ≤ √187
х ≥ √187 : (-3)
х ≥ - √(187/9)
х ≥ - √(20 7/9)
Так как -√25 < - √(20 7/9) < -√1, то
-1; -2; -3; -4 - целые отрицательные решения неравенства.
1) f(x)=7x-14, [0;4]
производная равна 7, 7≠0, , поэтому нет критических точек, и наибольшее и наименьшее свое значение функция принимает на концах отрезка.
f(0) = -14-наименьшее значение.
f(4) =14 наибольшее значение функции
2) f(x)= -0,2x + 0,4, [1;3]
аналогично 1) производная -0.2≠0, ищем значения функции на концах отрезка, т.е. f(1) =-0.2+0.4=0.2- наибольшее значение.
f(3) =-0.6+0.4=-0.2-наименьшее значение.
3) f(x)= 6/x, [1;6]
производная равна -6/х²≠0, не существует в точке 0, но эта точка не входит и в область определения. ищем значения функции на концах отрезка, т.е. f(1) =6/1=6- наибольшее значение.
f(6) =6/6=1- наименьшее значение.
4) f(x)= -5/x, [-5;-1]
Производная равна 5/х²≠0 не существует в точке 0, но эта точка не входит и в область определения. ищем значения функции на концах отрезка, т.е. f(-1) =-5/(-1)=5- наибольшее значение.
f(-5) =-5/(-5)=1- наименьшее значение.
Объяснение:
Разделим обе части неравенства на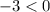 , знак неравенства при этом изменится на противоположный
, знак неравенства при этом изменится на противоположный
===========================
============================
Так как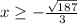 и
и 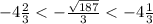 , то целые отрицательные решения неравенства
, то целые отрицательные решения неравенства