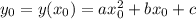Для решения данной задачи, нам необходимо подставить значение cos x=8/13 в выражение (sin x/2+cos x/2) + 2,8 и вычислить его.
По данному условию x∈(3π/2;2π), что означает, что x находится в интервале от 3π/2 до 2π.
Итак, начнем пошагово решать:
1. Для начала найдем значение sin x/2 и cos x/2.
При использовании половинного угла sin x/2 можно представить в виде √[(1 - cos x)/2], а cos x/2 как √[(1 + cos x)/2].
Подставим значение cos x=8/13 в формулы:
sin x/2 = √[(1 - cos x)/2] = √[(1 - 8/13)/2] = √[(5/13)/2] = √[5/26].
cos x/2 = √[(1 + cos x)/2] = √[(1 + 8/13)/2] = √[(21/13)/2] = √(21/26).
2. Теперь можно подставить найденные значения sin x/2 и cos x/2 в выражение (sin x/2+cos x/2) + 2,8:
Объяснение:
Если парабола задается уравнением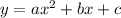 , то абсцисса вершины параболы
, то абсцисса вершины параболы 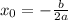
Для того, чтобы найти ординату вершины параболы, необходимо подставить найденную абсциссу в уравнение параболы: