Question

Решите уравнение: c^4 - c^3 + c^2 + c = 0

Answer 1

$0;\;\sqrt[3]{-\dfrac{17}{27}+\sqrt{\dfrac{11}{27}}}+\sqrt[3]{-\dfrac{17}{27}-\sqrt{\dfrac{11}{27}}}+\dfrac{1}{3}$

Объяснение:

$c^4 - c^3 + c^2 + c = 0\\c(c^3-c^2+c+1)=0$

$\left[\begin{array}{c}c=0\\c^3-c^2+c+1=0\end{array}\right,$

1)

$c=0$

2)

Путь $c=y+\dfrac{1}{3}$.

$\left(y+\dfrac{1}{3}\right)^3-\left(y+\dfrac{1}{3}\right)^2+\left(y+\dfrac{1}{3}\right)+1=0$

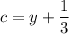Упростив выражение получим:

$y^3+\dfrac{2}{3}y+\dfrac{34}{27}=0$

По формуле Кардано, где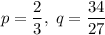 $p=\dfrac{2}{3},\;q=\dfrac{34}{27}$:

$y=\sqrt[3]{-\dfrac{17}{27}+\sqrt{\dfrac{11}{27}}}+\sqrt[3]{-\dfrac{17}{27}-\sqrt{\dfrac{11}{27}}}$

Обратная замена:

$c=\sqrt[3]{-\dfrac{17}{27}+\sqrt{\dfrac{11}{27}}}+\sqrt[3]{-\dfrac{17}{27}-\sqrt{\dfrac{11}{27}}}+\dfrac{1}{3}$

Уравнение решено!