В треугольнике одна сторона длиннее второй на 4, и короче третьей на 2.Р=23

👇

Увидеть ответ

Ответ:

LoveSmile78900987

25.03.2023

Одна сторона - первая; обозначим " а ".

Вторая " в".

Третья " с ".

Внимательно читаем условие. Из него видно, что самая короткая и наименьшая - "в",

"а" длиннее "в" на 4 единицы, но короче "с" на 2. Значит "с" - самая длинная.

Пусть "в"=х единиц длины, тогда

"а"=х+4, а "с"=х+4+2=х+6. Р(периметр)=а+в+с.

Р=(х+4) + х + (х+6)

3х+10=23

3х=23-10

3х=13

х=13 : 3. Это больше 4-х. Т.к. 12 : 3=4, а у нас 13.

Но меньше 5-ти. 15 : 3=5; а у нас 13.

Значит наименьшая сторона 4<x<5. Между 4 и 5. Найдем такой интервал среди предложенных.

Подходят А) 4<x<6

D) 3<x<5.

Это ответ.

4,7(95 оценок)

Открыть все ответы

Ответ:

Pleshkova01

25.03.2023

1. - B

т.к. k1=k2. Если они будут равными, тогда выполняется условие:

y=kx+l и y=kx+a

a=l. Т.е. l и a должны быть равны, однако тогда это уже будет совпадающая функция и не существует никаких других линейных функций, которые бы пересекали данную.

Если k1 не равно k2, тогда, естественно, линейные функции при определенном значении x и y могут иметь точки пересечения (думаю, не стоит объяснять почему уравнение с 2 переменными может иметь бесконечное множество решений)

2. С, т.к. x^2 умножается на -1, значит все его значения меняют знак

3. 1 - 3

2 - 4

необходимо подставлять под x значения, которые есть на графиках. Полученные координаты сравниваем с каждым рисунком. Необходимо, чтобы 2 точки совпадали (однако очень часто будут давать графики, которые сильно отличаются друг от друга, поэтому чаще всего достаточно найти 1 точку)

чертишь графики, их точка пересечения - это ответ.

чтобы начертить график, необходимо подставить вместо x какое-нибудь число. если функция линейная, достаточно найти 2 значения, например, x при 0 и x при 1 - между ними проводишь линию и у тебя готова функция.

ответ: (2;3)

5. а)

1 - любые числа

2 - x не равно 3, значит область определений принадлежит (-бесконечность; 3)U(3; +бесконечность)

б) плохо видно то, отрицательна ли двойка. если да:

f(-1)= -4+2 = -2

f(5)= 22

значит область значений принадлежит [-2;22]

если нет, тогда: [-6;18]

4,5(2 оценок)

Ответ:

mама

25.03.2023

Обратную матрицу найдем по формуле:

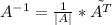$A^{-1}=\frac{1}{|A|}*\tilde{A^{T}}$ ,

где |A| - определитель матрицы, а 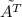$\tilde{A^{T}}$ - транспонированная матрица алгебраических дополнений

$|A|=\left[\begin{array}{ccc}2&3&-1\\1&-1&3\\3&5&1\end{array}\right]=-2+27-5-3-30-3=-16$

Т.к. определитель матрицы не равен 0, то обратная матрица существует.

Находим матрицу миноров. Для каждого элемента матрицы соответствующий ему минор вычисляется по определителю матрицы 2х2, которая получается вычеркиванием соответствующей строки и столбца для этого элемента:

$m_{11}=\left[\begin{array}{cc}-1&3\\5&1\end{array}\right]=-1-15=-16\\m_{12}=\left[\begin{array}{cc}1&3\\3&1\end{array}\right]=1-9=-8\\m_{13}=\left[\begin{array}{cc}1&-1\\3&5\end{array}\right]=5+3=8$

$m_{21}=\left[\begin{array}{cc}3&-1\\5&1\end{array}\right]=3+5=8\\m_{22}=\left[\begin{array}{cc}2&-1\\3&1\end{array}\right]=2+3=5\\m_{23}=\left[\begin{array}{cc}2&3\\3&5\end{array}\right]=10-9=1$

$m_{31}=\left[\begin{array}{cc}3&-1\\-1&3\end{array}\right]=9-1=8\\m_{32}=\left[\begin{array}{cc}2&-1\\1&3\end{array}\right]=6+1=7\\m_{33}=\left[\begin{array}{cc}2&3\\1&-1\end{array}\right]=-2-3=-5$

Получили следующую матрицу миноров:

$M=\left[\begin{array}{ccc}-16&-8&8\\8&5&1\\8&7&-5\end{array}\right]$

Из матрицы миноров получим матрицу алгебраических дополнений заменой знака на противоположный у элементов матрицы миноров, у которых сумма номеров строк и столбца нечетна:

$\tilde{A}=\left[\begin{array}{ccc}-16&8&8\\-8&5&-1\\8&-7&-5\end{array}\right]$

Следующим шагом получаем транспонированную матрицу алгебраических дополнений:

$\tilde{A^T}=\left[\begin{array}{ccc}-16&-8&8\\8&5&-7\\8&-1&-5\end{array}\right]$

Обратная матрица:

$A^{-1}=-\frac{1}{16}\left[\begin{array}{ccc}-16&-8&8\\8&5&-7\\8&-1&-5\end{array}\right]$

Проверим, что произведение исходной и обратной матрицы равно единичной:

$A*A^{-1}=-\frac{1}{16}\left[\begin{array}{ccc}2&3&-1\\1&-1&3\\3&5&1\end{array}\right]\left[\begin{array}{ccc}-16&-8&8\\8&5&-7\\8&-1&-5\end{array}\right]=-\frac{1}{16}*\left[\begin{array}{ccc}-16&0&0\\0&-16&0\\0&0&-16\end{array}\right]=\left[\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right]$