Постройте график функции у=х²+4х-2
Уравнение графика параболы со смещённым центром, ветви параболы направлены вверх.
Найдём координаты вершины параболы (для построения):
х₀= -b/2a= -4/2= -2
y₀= (-2)²+ 4*(-2) -2 =4 -8 -2= -6
Координаты вершины параболы (-2; -6)
Нужны дополнительные точки для построения графика. Придаём значения х, получаем значения у, составляем таблицу:
х -5 -4 -3 -2 -1 0 1
у 3 -2 -5 -6 -5 -2 3
По найденным точкам можно построить график параболы.
а)Подставляем в уравнение значение х=1,5 получаем у:
у=х²+4х-2
у= (1,5)² + 4*1,5 -2= 2,25+6-2= 6,25
б)Наоборот, заменяем у на 4:
у=х²+4х-2
х²+4х-2=4
х²+4х-6=0, квадратное уравнение, ищем корни:
х₁,₂=(-4±√16+24)2
х₁,₂=(-4±√40)2
х₁,₂=(-4±6,3)2
х₁=5,15
х₂=1,15
в)у=х²+4х-2
y <0
х²+4х-2<0
Решаем, как квадратное уравнение:
х²+4х-2=0
х₁,₂=(-4±√16+8)2
х₁,₂=(-4±√24)2
х₁,₂=(-4±4,9)2
х₁= -4,45
х₂= 0,45
у(х) <0 при -4,45 < х < 0,45
г)Функция возрастает на промежутке ( -2; ∞)
См. рисунок
1. Правильный шестиугольник, состоит из шести равносторонних треугольников.
Найдем сторону шестиугольника AB=r=48/6=8м.
Рассмотрим ΔСDO в нем CD=DO=0,5a (где а - сторона квадрата) ⇒ a=2CD
По теореме Пифагора найдем СD
r²=CD²+DO²=2CD² ⇒ r=CD√2⇒ м
м
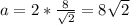 м
м
2. Из задачи №1. мы убедились, что радиус описанной окружности равен стороне правильного шестиугольника.
Площадь правильного шестиугольника равна
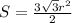 ⇒
⇒
 см
см
Длина окружности равна L=2πr=2π4√3=π*8√3≈43,5 см
3. Площадь сектора равна
 ≈151 см²
≈151 см²
(где n - градусная мера дуги сектора)

Формула:
Подставляем:
Решаем уровнение:
ответ:диагональ равна