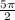 и
и 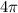 ]
] 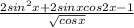
2sin²x+2sinxcos2x-1)/(√cosx)=(2sin²x+2sinxcos2x-1)/(√cosx)=
(2sinxcos2x-cos2x)/(√cosx)=cos2x(2sinx-1)/(√cosx)
ОДЗ : cosx>0;х∈(-π/2+2πm; π/2+2πm); m∈Z;
cos2x=0; х=π/4+πn/2; n∈Z;
sinx=1/2; х=(-1)ⁿπ/6+πк; n∈Z; его лучше расписать для четного и нечетного к. Если к четное , то к=2t; х=π/6+2πt ; t∈Z;
Если к нечетное , то к=2t + 1; х=5π/6+2πt ; t∈Z; этот ответ не подходит, т.к. не входит в ОДЗ.
Найдем корни уравнения из указанного отрезка.
а) х=π/4+πn/2; n∈Z;
2.5π≤π/4+πn/2≤4π; 2.5≤1/4+n/2≤4; 2.25≤n/2≤3.75; 4.5≤n/2≤7.5;
n=5; х=π/4+5π/2=∉ОДЗ,
n=6; х=π/4+6π/2=13π/4∉ОДЗ,
n=7; х=π/4+7π/2=15π/4
б) х=π/6+2πt ;
5/2≤1/6+2t≤4
5/2-1/6≤2t≤4-1/6
7/3≤2t≤23/6
7/6≤t≤23/12 нет здесь корней из указанного отрезка.
Объяснение:
1)у= 2x²-6x
2x²-6x=0
х(2х-6)=0
х₁=0
2х-6=0
2х=6
х₂=3
Строим график параболы. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу.
Таблица:
х -1 0 1 2 3 4
у 8 0 -4 -4 0 8
Смотрим на график и полученные значения х₁= 0 и х₂= 3.
Вывод: у<0 при х∈(0, 3)
(у меньше нуля при х от 0 до 3)
3)у= -3x²+5х
-3x²+5х=0
3x²-5х=0
х(3х-5)=0
х₁=0
3х-5=0
3х= 5
х₂= 5/3 (≈ 1,7)
Строим график параболы. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу.
Таблица:
х -2 -1 0 1 2 3
у -22 -8 0 2 -2 -12
Смотрим на график и полученные значения х₁= 0 и х₂=5/3.
Ветви параболы направлены вниз.
Вывод: у<0 при х∈(-∞, 0)∪(5/3, ∞)
(у меньше нуля от - бесконечности до 0 и от 5/3 до
+ бесконечности)
2)у= -x²+4x-4
-x²+4x-4=0
x²-4x+4=0, квадратное уравнение, ищем корни:
х₁,₂=(4±√16-16)/2
х₁,₂=(4±0)/2
х₁,₂=2
Строим график параболы. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу.
Таблица:
х -2 -1 0 1 2 3 4 5 6
у -16 -9 -4 -1 0 -1 -4 -9 -16
Смотрим на график и полученные значения х₁= 2 и х₂=2.
Ветви параболы направлены вниз.
Вывод: у<0 при х∈(-∞, 2)∪(2, ∞)
(у меньше нуля от - бесконечности до 2 и от 2 до
+ бесконечности)
4)y= -2x² -2,6х
-2x² -2,6х=0
2x² +2,6х=0
х(2х+2,6)=0
х₁=0
2х+2,6=0
2х= -2,6
х₂= -1,3
Строим график параболы. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу.
Таблица:
х -3 -2 -1 0 1 2
у -10,2 -2,8 0,6 0 -4,6 -13,2
Смотрим на график и полученные значения х₁= 0 и х₂= -1,3.
Ветви параболы направлены вниз.
Вывод: у<0 при х∈(-∞, -1,3)∪(0, ∞)
(у меньше нуля при х от - бесконечности до -1,3 и от 0 до
+ бесконечности)
1) y=3x^2-12x
0=3x^2-12x
3x^2-12x= 0
3x*(x-4)=0
x*(x-4) = 0
x=0
x-4=0
x=0
x=4
x1=0; x2=4
По графіку 1:
Корені (0;0) (4;0)
Область визначення x € R
Мінімум (2;-12)
Перетин з віссю ординат (0;0)
2) y=-2x³+5,2x
0=-2x³+5,2x
-2x³+5,2x= 0
-2x³+26/5x=0
-x*(2x²-26/5)=0
x*(2x²-26/5)=0
x=0
2x²-26/5=0
x=0
x=-√65/5
x=√65/5
x1=-√65/5; x2=0; x3=√65/5
x1≈-1,61245; x2=0; x3≈1,61245
По графіку 2:
Корені (-√65/5;0) (0;0)
(√65/5;0)
Область визначення x € R
Мінімум (-√195/15; -52√195/225
Максимум (√195/15; 52√195/225)
Перетин з віссю ординат (0;0)
3)y=-x²+6x-9
0=-x²+6x-9
0+x²-6x+9=0
(x-3)²=0
x-3=0
x=3
По графіку 3:
Корені (3;0)
Область визначення x € R
Максимум (3;0)
Перетин з віссю ординат (0;-9)
4)y=-x²-2,8x
0=-x²-2,8x
-x²-2,8x=0
-x²-14/5x=0
-x*(x+14/5)=0
x*(x+14/5)=0
x=0
x+14/5=0
x=0
x=-14/5
x1=-14/5 x2=0
x1=-2,8 x2=0
По графіку 4:
Корені (-14/5;0) (0;0)
Область визначення x € R
Максимум (-7/5; 49/25)
Перетин з віссю ординат (0;0)
Ниже↓
Объяснение:
Числитель 2sin²x+2sinx*cos2x-1=
=2sin²x+2sinx*(cos²x-sin²x)-(sin²x+cos²x)=
=sin²x- cos²x +2sinx*(cos²x-sin²x)=
=(sin²x- cos²x) -2sinx*(sin²x-cos²x)=
=(sin²x- cos²x)(1 -2sinx)= -( cos²x- sin²x)(1 -2sinx)=-cos2x(1 -2sinx). {-cos2x(1 -2sinx)=0
{cosx>0
Решим первое -cos2x(1 -2sinx)=0
1) cos2x=0, 2х=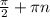 , х=
, х=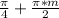 , m∈Z
, m∈Z
2) 1 -2sinx=0 , sinx=1\2 , х=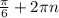 x=
x=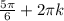 , n,к∈Z
, n,к∈Z
Решим второе
cosx>0 , х∈ (-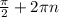 ;
; 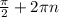 ). Выберем из найденных корней п 1, удовлетворяющие полученному условию. .
). Выберем из найденных корней п 1, удовлетворяющие полученному условию. .
Это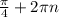 ,
, 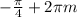 ,
, 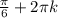 где n, m, k∈ Z
где n, m, k∈ Z
Выберем корни из [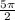 ;4π ]
;4π ]
Для х=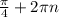 нет ,
нет ,
Для х=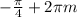 это
это 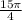 .
.
Для х=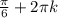 нет.
нет.