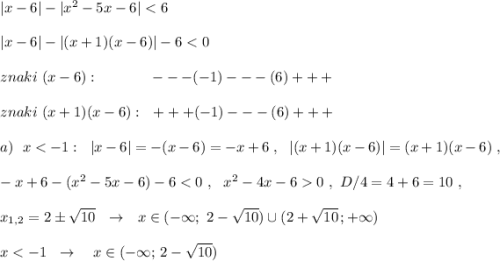
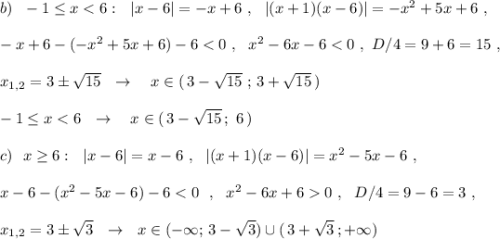
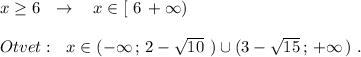
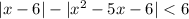
Преобразуем второй модуль и определим нули подмодульных выражений:
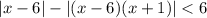
Нули подмодульных выражений: 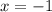 и
и  , поэтому раскрывать модуль будем на следующих промежутках:
, поэтому раскрывать модуль будем на следующих промежутках:
1) 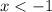
2) 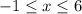
3) 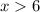
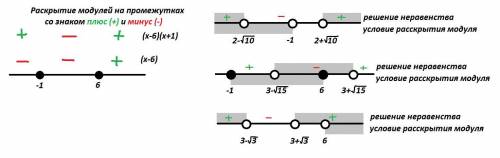
1) Раскрываем модуль на промежутке 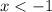 . Первый модуль раскрывается со сменой знака, второй - без смены знака:
. Первый модуль раскрывается со сменой знака, второй - без смены знака:
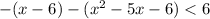
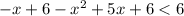
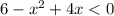
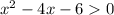
Найдем корни соответствующего уравнения:
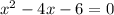
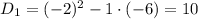
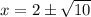
Методом интервалов найдем решение неравенства:
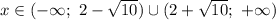
Учтем условие раскрытия модуля. Для этого сравним числа 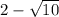 и
и 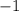 :
:
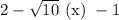
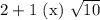
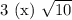
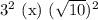
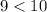
Значит, первое число меньше. Тогда, учитывая условие раскрытия модуля, получим:
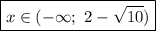
2) Раскрываем модуль на промежутке 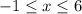 . Оба модуля раскрываются со сменой знака:
. Оба модуля раскрываются со сменой знака:
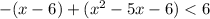
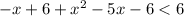
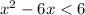
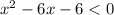
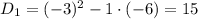
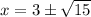
Методом интервалов найдем решение неравенства:
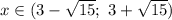
Учтем условие раскрытия модуля. Сравним числа 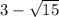 и
и 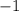 :
:
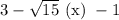
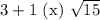
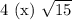
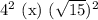
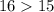
Первое число больше.
Сравним числа 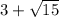 и
и 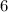 :
:
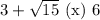
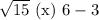
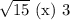
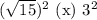
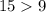
Первое число больше.
Теперь, учитывая условие раскрытия модуля, получим:
![\boxed{x\in(3-\sqrt{15} ;\ 6]}](/tpl/images/1359/2965/c2c24.png)
3) Раскрываем модуль на промежутке 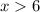 . Оба модуля раскрываются без смены знака:
. Оба модуля раскрываются без смены знака:


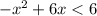
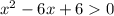
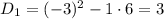
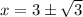
Используя метод интервалов, запишем решение неравенства:
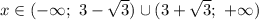
Число 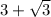 меньше числа
меньше числа 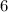 .
.
Запишем решение, учитывая условие раскрытия модуля:
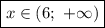
Итоговое решение неравенства представляет собой объединений трех промежутков:
![x\in(-\infty;\ 2-\sqrt{10} )\cup(3-\sqrt{15} ;\ 6]\cup(6;\ +\infty )](/tpl/images/1359/2965/d5f99.png)
Упростив запись, получим:
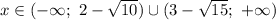
ответ: 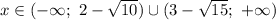
1. Упростите выражение
-12х+3ху-2(х+3ху)
-12x+3xy-2x-6xy= -14x-3xy
2. Из предложенных четырех пар чисел выбрите ту, которая является недопустимой для алгебраической дроби
2а²+3аb-b³
=b²-9a²>0 (b-3a)(b+3a) >0 видно что (3;1) так как =0
b²-9a²
3. Какое из четырех равенств не является тоджеством:
1. х³-8=(х-2)(х²+2х+4) Верно так как это разность кубов
2. х³+27=(х+3)(х²+3х+9) нет
3. х²-8х+16=(х-4)² да
4. х²+4ху+4у²=(х+2у)² да
(72²-28²)/(61²-39²) =(72-28)(72 + 28 )/ (61-39)(61+39)=2
4а⁷b¹⁵-4a⁵b¹⁷ 4a⁵b¹⁵(a²-b²) 2ab¹¹ (a-b)(a+b) -2ab¹¹ (a+b) = -2*3*-1*2=12
= = =
2a⁴b⁵-2a⁵b⁴ 2a⁴b⁴(b-a) -(a-b)
6.Преобразовав линейное уравнение 2х+3у-3=0 к виду линейной функции у=кх+м, найдите ее угловой коэффициент.
3y=3-2x
y=-2x/3+1
ответ -2/3
7.Найдите наибольшее значение функции у=3х-1 на отрезке [0,⅓]
f(0) = -1
f(1/3)=0
значит 0
8. Дана фунция у=f(x), где
| x², если -3≤ х ≤ 0;
|3x-1, если 0<х<2
|х, если х ≥ 2
Чему равно f(2)?
2 попадает на интервал x значит равна y=2
9.Какая из предложенных четырех пар чисел (x;y) является решением системы уравнений
|3x+y=7
|5x-8y=31
|y=7-3x
|5x-56+24x=31
|29x=87
|x=3
|y=-2
Для того, чтобы найти решение уравнения -15 = 3t(2 - t) мы начнем с того, что выполним открытие скобок в правой части уравнения.
Итак, откроем скобки и получим:
-15 = 3t * 2 - 3t * t;
-15 = 6t - 3t2;
3t2 - 6t - 15 = 0;
Разделим на 3 обе части уравнения и получим:
t2 - 2t - 5 = 0;
Вычислим прежде всего дискриминант уравнения:
D = b2 - 4ac = (-2)2 - 4 * 1 * (-5) = 4 + 20 = 24;
Вычислим корни уравнения следующим образом:
x1 = (-b + √D)/2a = (2 + √24)/2 * 1 = (2 + 2√6)/2 = 1 + √6;
x2 = (-b - √D)/2a = (2 - √24)/2 * 1 = (2 - 2√6)/2 = 1 - √6.