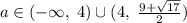у наиб = 795; у наим = - 89
Объяснение:
Функция
у = 9х² - х³ + 11
Производная функции
y' = 18x - 3x²
или
y' = 3х(6 - х)
Производная равна нулю в точках
х = 0 и х = 6
Знаки производной в интервалах
y' > 0 при x ∈ (0; 6)
y' < 0 при х ∈ (-∞; 0) ∪ (6; +∞)
В точке х = 0 имеет место локальный минимум функции уmin = 11
В точке х = 6 имеет место локальный максимум функции уmax = 119
Найдём значения функции в точках начала и конца заданного интервала х ∈ [-7; 10]
При х = -7 у = 9 · (-7)² - (-7)³ + 11 = 795
При х = 10 у = 9 · 10² - 10³ + 11 = -89
Сравнивая полученные результаты со значениями функции в точках локальных минимума и максимума, находим. что
у наиб = 441
у наим = - 89
В решении.
Объяснение:
Решить неравенство методом интервалов:
5) (х + 10)/(х - 11) <= 0
Приравнять к нулю и решить уравнение:
(х + 10)/(х - 11) = 0
х + 10 = 0
х₁ = -10;
х - 11 = 0
х₂ = 11;
Начертить числовую прямую и отметить на ней схематично вычисленные корни.
-∞ + -10 - 11 + +∞
Определить знак самого правого интервала, для этого придать любое значение х больше 11 и подставить в неравенство:
х = 12;
(12 + 10)/(12 - 11) = 22/1 > 0, значит, плюс.
Влево знаки меняются через корень.
Обозначить знаки интервалов у числовой прямой.
Неравенство < 0, значит, решениями будут интервалы со знаком минус.
Решение неравенства: х∈[-10; 11).
Неравенство нестрогое, скобка квадратная.
Значение х = 11 на числовой прямой с незакрашенным кружочком, а в решении под круглой скобкой, так как это корень знаменателя.
6) (х - 6)(х + 12)/(х - 5) < 0
Приравнять к нулю и решить уравнение:
(х - 6)(х + 12)/(х - 5) = 0
(х - 6)(х + 12) = 0
х - 6 = 0
х₁ = 6;
х + 12 = 0
х₂ = -12;
х - 5 = 0
х₃ = 5;
Начертить числовую прямую и отметить на ней схематично вычисленные корни.
-∞ - -12 + 5 - 6 + +∞
Определить знак самого правого интервала, для этого придать любое значение х больше 6 и подставить в неравенство:
х = 10;
(10 - 6)(10 + 12)/(10 - 5) = 88/5 > 0, значит, плюс.
Влево знаки меняются через корень.
Обозначить знаки интервалов у числовой прямой.
Неравенство < 0, значит, решениями будут интервалы со знаком минус.
Решения неравенства: х∈(-∞; -12)∪(5; 6).
Неравенство строгое, скобки круглые.
Пусть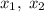 — решения уравнения
— решения уравнения 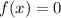 . По условию
. По условию 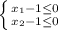 . Можно сделать замену:
. Можно сделать замену: 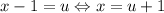 и рассмотреть функцию
и рассмотреть функцию 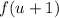 . Переформулируем условие: найти все значения параметра
. Переформулируем условие: найти все значения параметра  , при каждом из которых уравнение
, при каждом из которых уравнение 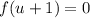 имеет два различных неположительных решения.
имеет два различных неположительных решения.
Теперь нужно наличие двух различных решений. Здесь удобно вернутся к изначальному уравнению (так как мы просто двигали параболу горизонтально).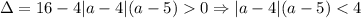 , это неравенство эквивалентно системе:
, это неравенство эквивалентно системе: 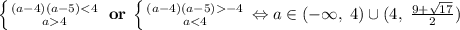 (2).
(2).
Пересекая (1) с (2) получим ответ.
ответ: