Выполняю задание по Вашей
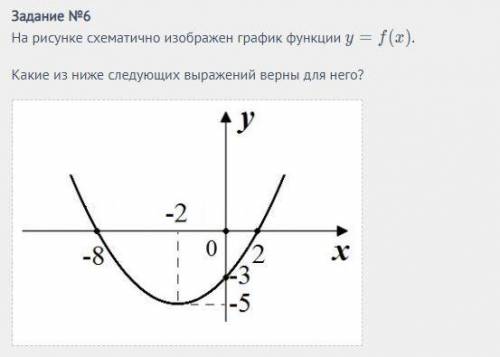
1.f(-3)=0 неверно, т.к. абсциссе х=-3 соответствует отрицательная ордината, а не нуль.
2. D=0, неверно. если бы дискриминант равнялся нулю, то парабола касалась бы оси ох в одной точке, а если она пересекает ось в двух точках, то дискриминант больше нуля, и абсциссы точек пересечения параболы с осью ох - нули функции, или корни уравнения f(х)=0 , видим два различных корня это х=-8, х=2.
3. f(х)≤0, это утверждение верно, т.к. при х ∈[-8;2] все значения у меньше или равны нулю. как указал выше, у равен нулю в концах отрезка х=-8 и х=2, а остальные значения у =f(х) меньше нуля, т.е. график находится ниже оси ох.
4. о дискриминанте говорили. нет. не верно, т.к. если бы дискриминант был меньше нуля, то с осью ох график бы не пересекался.
5. проведем мысленно прямую у=-5, с графиком она касается в одной точке, поэтому утверждение верно, корень уравнения х=-2
6. это не верно, т.к. парабола и прямая у=-3 пересекаются в двух точках, значит, уравнение имеет два решения.
7. дискриминант больше нуля, верно, что указывает на количество корней уравнения, их два различных корня, если D>0, а конкретнее, х=-8 и х=2.
4
Объяснение:
Теорема 1 (первый признак равенства — по двум катетам)
Если катеты одного треугольника соответственно равны катетам другого треугольника, то такие прямоугольные треугольники равны.
Теорема 2 (второй признак равенства — по катету и прилежащему острому углу)
Если катет и прилежащий острый угол одного треугольника соответственно равны катету и прилежащему острому углу другого треугольника, то такие прямоугольные треугольники равны.
Теорема 3 (третий признак равенства — по гипотенузе и острому углу)
Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны.
Теорема 4 (четвёртый признак равенства — по гипотенузе и катету)
Если гипотенуза и катет одного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие прямоугольные треугольники равны.
#1.
Пусть первое число - x; а второе число - y. Получим два уравнения:

Выразим x через y и подставим это значение в первое уравнение:

По теореме Виета:

Так как мы знаем, что оба числа положительные, то y = 13
Найдем x:
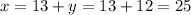
ответ: 12, 25.
#2.
Периметр - это сумма всех сторон; формула - 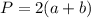
Найдем сумму длины и ширины:
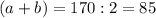
Отсюда можно выразить длину b:

Диагонали в прямоугольнике образуют два равных прямоугольных треугольника, где диагонали - гипотенузы, а стороны - катеты.
Найдем длину одной диагонали:
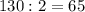
По теореме Пифагора:
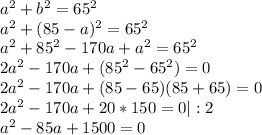
По теореме Виета:

Если a = 25, то b = 60, и наоборот. Длины сторон - 25 и 60 см.
ответ: 25, 60.
Правильные утверждения:
3) решением неравенства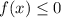 является отрезок
является отрезок ![[\, -8\, ;\, 2\ ]](/tpl/images/1359/3483/379aa.png) ;
;
5) уравнение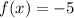 имеет одно решение, это решение
имеет одно решение, это решение  , так как
, так как 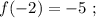
7)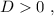 так как имеется две точки пересечения параболы с осью ОХ, то есть уравнение
так как имеется две точки пересечения параболы с осью ОХ, то есть уравнение 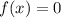 имеет два корня .
имеет два корня .