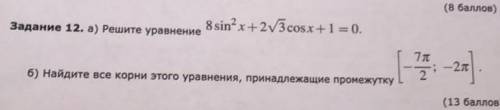
![8sin^2x+2\sqrt3\, cosx+1=0\\\\8(1-cos^2x)+2\sqrt3\, cosx+1=0\\\\8cos^2x-2\sqrt3\, cosx-9=0\\\\D/4=3+72=75\ \ ,\ \ cosx=\dfrac{\sqrt3\pm 5\sqrt3}{8}\\\\a)\ \ cosx=-\dfrac{\sqrt3}{2}\ \ ,\ \ x=\pm \dfrac{5\pi }{6}+2\pi n\ ,\ n\in Z\\\\b)\ \ cosx=\dfrac{3\sqrt3}{4}\approx 1,2991\ \ \Rightarrow \ \ x\in \varnothing \\\\\\c)\ \ x\in \Big[\, -\dfrac{7\pi}{2}\ ;\ -2\pi \ \Big]](/tpl/images/1359/8689/a12ac.png)
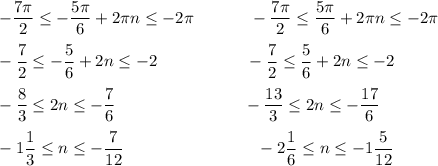
![{}\ \ \ n=-1\in Z\qquad \qquad \qquad \qquad \ \qquad \qquad \ n=-2\in Z\\\\x=-\dfrac{5\pi}{6}-2\pi =-\dfrac{17\pi}{6}\qquad \qquad \qquad \ \ x=\dfrac{5\pi}{6}-4\pi =-\dfrac{19\pi}{6}}\\\\Otvet:\ \ 1)\ x=\pm \dfrac{5\pi}{6}+2\pi n\ ,\ n\in Z\ \ ;\ \ 2)\ x=-\dfrac{17\pi}{6}\ ,\ -\dfrac{19\pi}{6}\in \Big[\, -\dfrac{7\pi}{2}\, ;\, -2\pi \, \Big]\ .](/tpl/images/1359/8689/0c154.png)
(-∞ ;-3) => функция выпукла;
(-3; +∞) => функция вогнута;
(-∞ ;-6) <=> f'(x) > 0 => функция возрастает;
(-6; 0) <=> f'(x) < 0 => функция убывает;
(0; +∞) <=> f'(x) > 0 => функция возрастает ;
Объяснение:
1. Находим интервалы возрастания и убывания. Первая производная.
f'(x) = 3x2+18x
или
f'(x)=3x(x+6)
Находим нули функции. Для этого приравниваем производную к нулю
x(x+6) = 0
Откуда:
x1 = 0
x2 = -6
(-∞ ;-6) <=> f'(x) > 0 => функция возрастает;
(-6; 0) <=> f'(x) < 0 => функция убывает;
(0; +∞) <=> f'(x) > 0 => функция возрастает ;
В окрестности точки x = -6 производная функции меняет знак с (+) на (-). Следовательно, точка x = -6 - точка максимума. В окрестности точки x = 0 производная функции меняет знак с (-) на (+). Следовательно, точка x = 0 - точка минимума.
2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная.
f''(x) = 6x+18
Находим корни уравнения. Для этого полученную функцию приравняем к нулю.
6x+18 = 0
Откуда точки перегиба:
x1 = -3
(-∞ ;-3) => функция выпукла;
(-3; +∞) => функция вогнута;
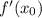производная функции в данной точке. А 
точка касания по иксу.
мы должны найти производную общего типа этой функции.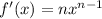
- где n это степень.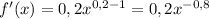
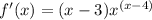
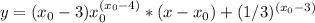
и получаешь уравнение касательной.
