
Построим это число поцифренно. Для этого, воспользуемся одним из условий задачи: если n цифра в этом числе, то следующая цифра не может быть равна n-1, n или n+1.
К тому же, нужно выберать минимально возможную цифру (так как нам нужно минимально число).
Начнем с первой цифры. Для этого выберем минимально возможную (и отличную от нуля) - цифру 1.
Вторая цифра не может быть 0, 1 или 2. Поэтому минимально возможная цифра - цифра 3.
Третью цифру выбераем таким же цифра 0.
Четвертую и пятую цифру, выбераем тем же с дополнительным условием - их сумма должна быть 17-1-3-0=13. Следовательно, четвертая цифра - цифра 4, а пятая цифра - цифра 9.
Откуда заключаем, что наше число - 13049
1. Пусть первый тракторист может самостоятельно выполнить задание за х часов, а второй за (х+7) часов,зная, что вместе они могут выполнить задание за 12 часов, имеем уравнение:
12x+84+12x-x^2-7x=0
x^2-17x-84=0
2. а-производительность первой трубы
b-производительность второй трубы
c-произовдительность третьей трубы
d-производительность четвертой трубы
a+b+c=1/105
a+b+d=1/75
c+d=1/175
складываем эту систему
получаем:
2a+2b+2c+2d=1/105+1/75+1/175
2(a+b+c+d)=1/35
a+b+c+d=70
итого, 70 минут, 1 час 10 минут
ответ: 1 ч 10 мин
x1=21, x2=-4 - не удовлетворяет условию задачи
Значит первый тракторист выполнить задание самостоятельно за 21 час, а второй - за 28 часов
ответ: 21 час и 28 часов.
19.
Замена переменной:
u=4; v=2
сложения: 2х=8; x=4; y=0
О т в е т. (4;0)
20.
О т в е т.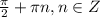 ;
; 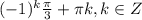
Отрезку [2π; 3π] принадлежат корни: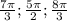
21.
ОДЗ: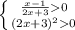
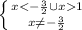
x∈(-∞; -1,5) U(1;+∞)
По свойству логарифма степени:
Заменим сумму логарифмов логарифмом произведения:
Логарифмическая функция с основанием 2 возрастающая, поэтому
x∈(-∞;-1] U[3;+∞)
Найденные решения входят в ОДЗ,
О т в е т. (-∞;-1] U[3;+∞)