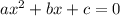
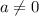, так как уравнение обращается в линейное.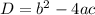
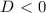уравнение не имеет решений (вообще имеет, но это в школе не проходят).
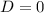то уравнение имеет 1 решение (корень).
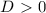- уравнение имеет 2 корня.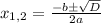
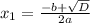
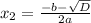
Чтоб найти числовое значение многочлена a2+2ay+y2 при a=8 и y=−7, нужно в выражение подставить известные значения а и у, и решить его.
а2 + 2ау + у2 = (8)2 + 2 * 8 * (- 7) + (- 7)2;
Возносим (8) и (- 7) квадрату:
(8)2 = 64;
(- 7)2 = 49;
Умножаем:
2 * 8 * (- 7) = 16 * (- 7) = - 112;
Подставляем значения в выражение:
64 + (- 112) + 49;
Раскрываем скобки:
64 - 112 + 49;
Вычитаем:
64 - 112 + 49 = - 48 + 49;
Добавляем:
- 48 + 49 = 1.
ответ: числовое значение многочлена a2+2ay+y2 при a=8, y=−7 равен 1
(4; 1)
Объяснение:
Система уравнений:
√(x-3)=y, где x-3≥0
y+|x-3|=2; y=2-|x-3|
√(x-3)=2-|x-3|
При x-3≥0:
√(x-3)=2-x+3
√(x-3)=5-x
√(x-3)²=(5-x)²
x-3=25-10x+x²
x²-10x+25-x+3=0
x²-11x+28=0; D=121-112=9
x₁=(11-3)/2=8/2=4
x₂=(11+3)/2=14/2=7
y₁=√(4-3)=1; y₁=2-|4-3|=1
y₂=√(7-3)=2; y₂=2-|2-3|=2-1=1
Отсюда следует, что этой системы корнями будут x=4 и y=1.