
Объяснение:
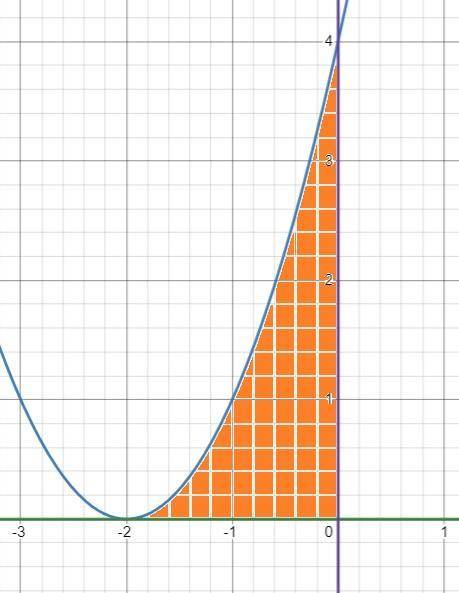
1) Строем графики функций y=(x+2)²;y=0; x=0.
Площадь S=∫₋₂⁰(x+2)² dx=> u=x+2; du=dx=> ∫₀²u²du=u³/3| ₀²=
=2³/3-0³/3=8/3. (См. скриншот 1-30...)
-------------------
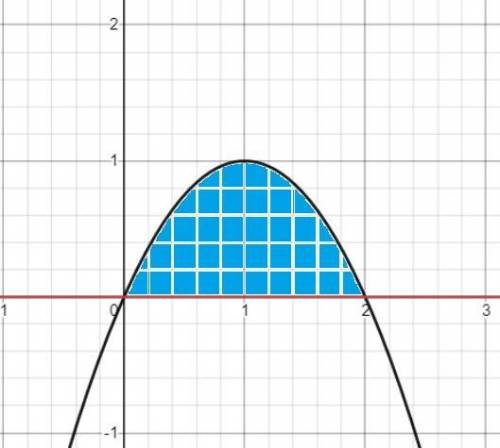
2) Строем графики функций y=2x-x²; y=0.
Площадь ∫₀²(2x-x²)dx=2∫₀²xdx-∫₀²x²dx =2*1/2x²|₀² - 1/3x³|₀²=4-8/3= 4/3.
(См скриншот 2-30...)
-----------------------
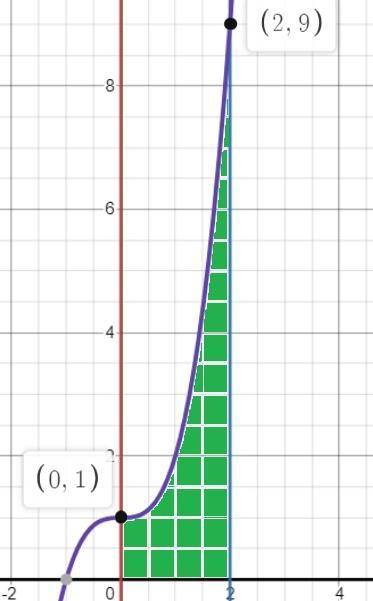
3) Строем графики функций y=x³+1; y=0; x=0; x=2.
Площадь ∫₀²(x³+1)dx=1/4x⁴|₀²+x|₀²=1/4*16+2=6. (См. скриншот 3-30...)
---------------------
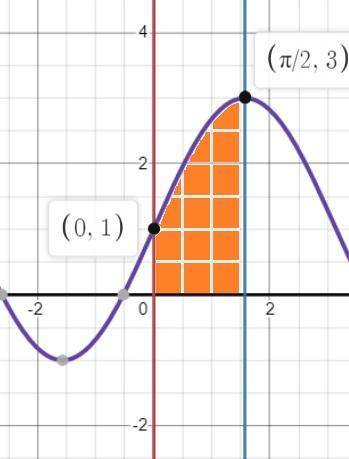
4) Строем графики функций y=1+2sinx; y=0; x=0; x=π/2.
Площадь ∫₀π/2(1+2sinx)dx= -2cosx|₀π/2 + x|₀π/2=2+π/2 = (4+π)/2.
(См. скриншот 4-30...)
1. Напишите уравнение прямой, проходящей через заданные точки: A (2; 1) B (-1; 2). [2 балла]
2. Найти координаты и радиус центра круга в соответствии с заданным уравнением: (x-4) 2 + (y + 8) 2 = 36 [1 балл]
3. Очки даны.
а) опираться на координаты потолков; [1 балл]
б) найти длину стен; [3 балла]
в) определить тип (равносторонний, равносторонний, прямоугольный); [2 балла]
г) Рассчитать площадь данного треугольника. [2 балла]
4. Найдите площадь прямоугольника с вершинами A (1; -1) B (0; 1) C (4; 3) и D (5; 1) и докажите, что это прямоугольник. Сделать это:
а) нарисуйте схему координат потолков; [1 балл]
б) найти длину стен; [4 балла]
в) определить и доказать диагонали; [2 балла]
г) Рассчитайте площадь прямоугольника. [2 балла]
Объяснение:
памагитеее