Question

Докажите, что число 1+1/2+1/3+...+1/m не целое

Answer 1

Пусть сумма ряда :

$1 +\frac{1}{2} +\frac{1}{3} +\frac{1}{4} ...+\frac{1}{m} =S$

Предположим, что число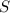 $S$ - целое число и $m\geq2$

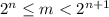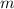Найдем среди чисел от 1 до m наибольшую степень двойки, то есть такую, что : $2^n\leq m$ , где $m$ - натуральное число.

Умножим обе части равенства на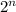 $2^n$ :

$2^n +\frac{2^n}{2} +\frac{2^n}{3} +...+\frac{2^n}{2^n} +...+\frac{1}{m} =2^nS\\\frac{2^n}{2} +\frac{2^n}{3} +...+\frac{2^n}{2^n -1}+\frac{2^n}{2^n +1} +...+\frac{1}{m} = 2^n(S-1) - 1$

Поскольку число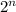 $2^n$ имеет максимальную степень двойки для чисел от 1 по m, то все степени двоек входящие в разложение на простые множители чисел от 1 по m, если таковые существуют, сократятся c числителем

$a$ - натуральное нечетное число.

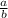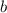Приведем все дроби к наименьшему общему знаменателю, но поскольку,  наименьший общий знаменатель нечетных чисел число нечетное, а все числители четные, то левая часть равенства будет выглядить так :  $\frac{a}{b}$ , где $a$ - четное число, $b$ - нечетное число.

Целое число: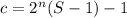  $c=2^n(S-1) - 1$   является нечетным при $n\geq1$.

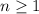Тогда :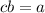 $cb=a$  произведение двух нечетных числе число нечетное, но число $a$ - четное .

То есть мы пришли к противоречию, а значит число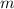 $m$- нецелое.

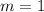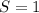Если же $m=1$ , то $S= 1$ - целое число.

Примечание: данное доказательство работает не только для данного ряда, но и  для любого упорядоченного ряда вида :

$\frac{1}{a_{1} } + \frac{1}{a_{2} } +\frac{1}{a_{3} }...+\frac{1}{a_{n} }$ , если в этом ряду существует число вида $a_{k} =qp^m$ ,где $p$ - простое, $q$ не делится на $p$ , причем в разложении на простые множители каждого из чисел от $a_{1}$ до $a_{n}$  содержится не более чем $m-1$- я cтепень числа $p$ , за исключением самого числа $p^m$ .  То есть умножаем обе части на $p^m$ и также рассуждаем про делимость на $p$ .