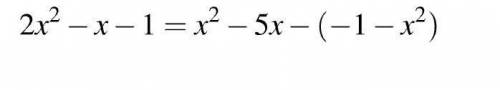
ответ
а) -3х2 (-х3 + х - 5) = 3х2 • х3 - 3х2 • x + 3х2 • 5 = 3х5 - 3х3 + 15х2;
б) (1 + 2а - а2) • 5а = 1 • 5a + 2a • 5a - а2 • 5a = 5a + 10а2 - 5a3;
в) 2/3 x2y(15x - 0,9y + 6) = 2/3x2y • 15x - 2/3x2y • 0,9у + 2/3x2y • 6 = 10x3y - 0,6x2y2 + 4х2y;
г) 3а4x(а2 - 2ах + х3 - 1) = За4х • а2 - За4х • 2ах + + За4х • х3 - За4х • 1 = За6х - 6а5х2 + За4х4 - За4х;
д) (х2у - ху + ху2 + у3) • Зху2 = х2у • Зху2 - ху • Зху2 + ху2 • Зху2 + y3 • Зху2 = Зx3y3 - Зx3y3 + Зх2у4 + Зху5;
е) -3/7а4(2,1b2 - 0,7а + 35) = -3/7а4 • 2,1b2 + 3/7а4 • 0,7а - 3/7а4 • 35 = -0,9а4b2 + 0,3а5 - 15а4.
Объяснение:
5/8 и 4/9 . Общий знаменатель 8*9=72. Дополнительные множители 9 и 8 соответственно.
45/72 и 32/72.
***
11/24 и 101/180 . Разложим на множители 24= 2*2*2*3; 180=2*2*3*3*5
Общий знаменатель 180*2=360 (недостающий множитель из разложения числа 24). Дополнительные множители 15 и 2 соответственно. получаем
11*15/24*15 и 101*2/180*2.
165/360 и 202/360.
***
5/12 и 23/27. 12=2*2*3. 27=3*3*3. Общий знаменатель 27*4=108. дополнительные множители 108/12=9 и 108/27=4.
Получим: 5*9/12*9 , 23*4/27*4
45/108 и 92/108.
Раскрываем скобки в правой части:
2х² - х - 1 = х² - 5х + 1 + х²
Переносим все элементы из правой части в левую с противоположными знаками:
2х² - х - 1 - х² + 5х - 1 - х² = 0
Сокращаем и получаем линейное уравнение:
4х - 2 = 0
4х = 2
х = 0,5
ответ: 0,5