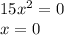![A(0,1,-1)\ \ ,\ \ B(1,-1,2)\ \ ,\ \ C(3,1,0)\ \ ,\ \ D(2,-3,1)\\\\\alpha =(\, \widehat {AB\, ;\, BCD}\ )\\\\\Big[\, \overline {BC}\times \overline {BD}\, \Big]=\left|\begin{array}{ccc}i&j&k\\2&2&-2\\1&-2&-1\end{array}\right|=\vec{i}\cdot (-2-4)-\vec{j}\cdot (-2+2)+\vec{k}\cdot (-4-2)=\\\\\\=-6\vec{i}-0\vec{j}-6\vec{k}\\\\\vec{n}=-\dfrac{1}{6}\cdot \Big[\, \overline {BC}\times \overline {BD}\, \Big]=(1\, ;\, 0\, ;\, 1)\\\\\vec{s}=\overline {AB}=(1,-2,3)](/tpl/images/1360/4632/f5966.png)
В решении.
Объяснение:
Дана функция y = -5x+2.
Найти:
а)значение у,при котором х= -3;
Подставить значение х в уравнение и вычислить у:
y = -5x+2; х= -3.
у = -5 * (-3) +2
у = 15 + 2
у = 17.
При х = -3 у = 17.
б) значение х, при котором значение у=1;
Подставить значение у в уравнение и вычислить х:
y = -5x+2; у = 1.
1 = -5х + 2
5х = 2 - 1
5х = 1
х = 1/5
х = 0,2.
При х = 0,2 у = 1.
в) координаты точек пересечения графика данной функции с осями координат;
При пересечении графиком оси Ох у=0;
-5x+2 = 0
-5х = -2
х= -2/-5
х = 0,4.
Координаты точки пересечения графиком оси Ох (0,4; 0).
При пересечении графиком оси Оу х=0;
у = -5 * 0 + 2
у = 2.
Координаты точки пересечения графиком оси Оу (0; 2).
г) определить взаимное расположение графика данной функции с графиками функций у=6; у=-5х+4; у=3х+2.
y = -5x+2; у = 6, пересекутся, k₁ ≠ k₂;
y = -5x+2; у = -5х+4 параллельны, k₁ = k₂, b₁ ≠ b₂.
y = -5x+2; у = 3х+2, пересекутся, k₁ ≠ k₂.
Ремарка:
в большинстве случаев использовалась расширенная теорема Виета, которая есть не что иное как счелканье уравнений как семечек в уме. Я рекомендую вам изучить очень хорошо метод переброски, который, поверьте моему опыту, упростит вам жизнь.
Объяснение:
1)
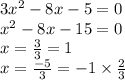
2)
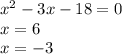
3)
4)
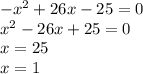
5)
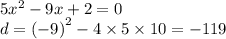
То есть уравнение корней не имеет, так как дискриминант отрицательный.
6)
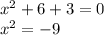
Уравнение корней не имеет, так как какое бы мы число к квадрату не поднесли, результат всегда будет положительный, а не отрицательный, как вот (-9).
7)
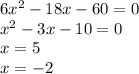
8)
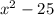
Если задача стоит разложить на множители, то имеем:
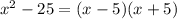
Если задача стоит найти корни уравнения, то имеем:
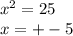
9)
Уравнение не имеет корней, так как левая часть всегда > 0, а не равна ему. Действительно, какое бы мы число не подставили вместо x, оно всегда будет ≥ 80.
10)
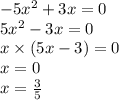
11)
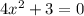
Уравнение не имеет корней, аналогичная ситуация как в уравнении 9.
12)