1. log₂(x+1)<log₂(6-2x) ОДЗ: x+1>0 x>-1 6-2x>0 x<3 ⇒ x∈(-1;3)
x+1<6-2x 3x<5 x<5/3=1²/₃.
ответ: x∈(-1;1²/₃).
2.lg(x-3) >0 ОДЗ: x-3>0 x>3.
lg(x-3)>lg1 x-3>1 x>4.
ответ: x∈(4;+∞).
3. log₅((3-x)/(2-x))<1 ОДЗ: -∞__+__2__-__3__+__+∞ ⇒ x∈(-∞;2)U(3;+∞)
log₅((3-x)/(2-x))<log₅5 (3-x)/(2-x)<5 3-x<10-5x 4x<7 x<7/4=1³/₄
ответ: x∈(-∞;1³/₄).
4. log₃₃(33x+2)≤1 ОДЗ: 33x+2>0 33x>-2 x>-2/33
log₃₃(33x+2)≤log₃₃33
33x+2≤33 33x≤31 x≤31/33
ответ: x∈(-2/33;31/33].
5. log₁/₉(2x-1)+log₁/₉(x)>0 ОДЗ: 2x-1>0 x>1/2 x>0 ⇒ x>1/2=0,5
log₁/₉((2x-1)*x)>log₁/₉1
(2x-1)*x<1 2x²-x-1<0 D=9 x₁=1 x₂=-0,5 ⇒
(x-1)(x+0,5)<0 -∞__+__-0,5__-__1__+__+∞ ⇒ x∈(-0,5;1).
ответ: x∈(0,5;1).
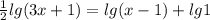
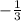, x > 1 ⇒ x > 1. 
при условии существования логарифмов. В нашем случае это тоже работает: данные логарифмы десятичные, значит, в основании 10. Вспомним, что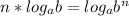 
(также при условии существования логарифма). Сразу вычислим lg1 - чтобы получить из 10 1, нужно 10 возвести в нулевую степень, значит, что 0. Тогда наше уравнение равносильно такому: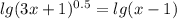 
х км/ч- скорость первого бегуна , тогда (x+7)км/ч -скорость второго бегуна. второй бегун пробежал круг за 1/2-1/6=2/6=(1/3 )часа. где 10 мин.=10/60=1/6часа. При этом через 0.5часа после старта первому бегуну оставалось 0.5 км до окончания первого круга . Составим уравнение:
(1/3*)(х+7)-0.5х=0.5
(1/3)х+7/3-0.5х=0.5;
-1/6х=-11/6
х=11
11км/ч-скорость первого бегуна.