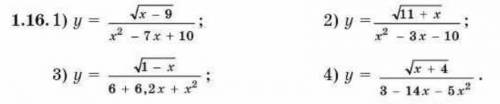
нехай перший рухався зі швидкістю х км/год, а другий у км/год. тоді перший пройшов до зустрічі 3х км, а другий 3у км., а разом 3х+3у=27 км за умовою перший прийшов на 1 год 21 хв=1,35 год раніше. тому 27/у-27/х=1,35 складемо систему рівнянь [latex] \left \{ {3x+3y=27} \atop {27/y-27/x=1.35}} \right. [/latex] виразимо в першому рівнянні х через у х=9-у підставимо в друге рівняння 20х-20у=ху . маємо: 180-20у-20у=9у-у² у²-49у+180=0 d=1681 y1=(49+41)/2=45 y2=4 тоді x1=9-45=-36 , що не задов умові і х2=9-4=5 км/год швидкість першого пішохода 5 км/год, а другого 4 км/год
Объяснение:
1)
х-9≥0
х≥9;
х²-7х+10≠0
(х-2)(х-5)≠0
х≠2; х≠5;
х€[9;∞)
2)
11+х≥0
х≥-11;
х²-3х-10≠0
(х-5)(х+2)≠0
х≠5; х≠-2;
х€[-11;-2)U(2;5)U(5;∞);
3)
1-x≥0
x≤1;
x²+6,2+6≠0
при любом х знаменатель положительный;
тогда х€(-∞;1];
4)
х+4≥0
х≥-4;
5х²+14х-3≠0
(х+3)(5х-1)≠0
х=-3; х=0,2;
х€[-4;-3)U(3;0,2)U(0,2;∞);