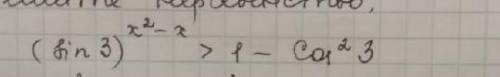
Объяснение:
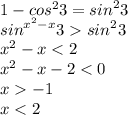
(-1;2)
Число делится на 10 только в том случае, если оно оканчивается цифрой 0.
Посмотрим, какой цифрой оканчивается каждое слагаемое.
1) число 7 в разных степенях оканчивается разными цифрами. Попробуем установить закономерность.
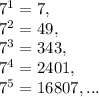
Т.е. последние цифры записи степеней семерки чередуются так: 7 - 9 - 3 - 1 и по кругу.
Т.к.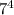 
оканчивается цифрой 1, то 
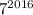также оканчивается цифрой 1. Тогда число 
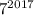оканчивается цифрой 7.
2) Для степеней четверки закономерность проще - 4 - 6 и по кругу:
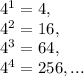
Поскольку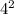 
оканчивается цифрой 6, то 
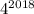также оканчивается цифрой 6.
3) Закономерность для степеней тройки - 3 - 9 - 7 - 1 и по кругу:
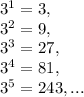
Т.к.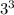 
оканчивается цифрой 7, то 
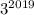также оканчивается цифрой 7.
В итоге слагаемые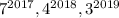 
оканчиваются цифрами 7, 6 и 7 соответственно. Если их сложить, то в разрядке единиц класса единиц получим 0. Т.е. число 
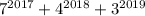оканчивается цифрой 0 - следовательно, оно таки делится на 10.
ОТВЕТ: да.
(4; -20; 20); (4; -12; 4)
Объяснение:
|f(1)| = |a*1^2+b*1+c| = |a+b+c| = 4
Это значит два варианта:
a+b+c = -4
a+b+c = 4
|f(2)| = |a*2^2+b*2+c| = |4a+2b+c| = 4
Это опять два варианта:
4a+2b+c = -4
4a+2b+c = 4
|f(3)| = |a*3^2+b*3+c| = |9a+3b+c| = 4
И тут два варианта:
9a+3b+c = -4
9a+3b+c = 4
Квадратная функция не может иметь одинаковое значение в 3 точках.
Поэтому варианты (-4;-4;-4) и (4;4;4) сразу отпадают.
И помним, что а > 0, поэтому ветви параболы направлены вверх.
Если вершина между 2 и 3, и в них обоих значение -4, то в 1 должно быть 4.
{ a+b+c = 4
{ 4a+2b+c = -4
{ 9a+3b+c = -4
Умножаем 1 уравнение на -4 и складываем со 2 уравнением.
Умножаем 1 уравнение на -9 и складываем с 3 уравнением.
{ a+b+c = 4
{ 0a-2b-3c = -20
{ 0a-6b-8c = -40
Умножаем 2 уравнение на -3 и складываем с 3 уравнением.
{ a+b+c = 4
{ 0a-2b-3c = -20
{ 0a+0b+c = 20
Получили с = 20. Подставляем во 2 уравнени.
-2b - 3*20 = -20; -2b = 40; b = -20
Подставляем в 1 уравнение
a - 20 + 20 = 4; a = 4
Решение: (4; -20; 20)
Если вершина между 2 и 3, и в них обоих 4, то в 1 должно быть больше 4. Не подходит.
Если вершина между 1 и 2, и в них обоих 4, то в 3 должно быть больше 4. Не подходит.
Если вершина между 1 и 2, и в них значение -4, то в точке 3 должно быть 4.
{ a+b+c = -4
{ 4a+2b+c = -4
{ 9a+3b+c = 4
Умножаем 1 уравнение на -4 и складываем со 2 уравнением.
Умножаем 1 уравнение на -9 и складываем с 3 уравнением.
{ a+b+c = -4
{ 0a-2b-3c = 12
{ 0a-6b-8c = 40
Умножаем 2 уравнение на -3 и складываем с 3 уравнением.
{ a+b+c=-4
{ 0a-2b-3c = 12
{ 0a+0b+c = 4
Получили с = 4. Подставляем во 2 уравнение
-2b - 3*4 = 12; -2b = 24; b = -12
Подставляем в 1 уравнение
a - 12 + 4 = -4; a = 12 - 4 - 4 = 4
Решение: (4; -12; 4)
Решение задания прилагаю