3) f(x)= 1. Сначала находим область определения этой функции. Функция задана многочленом, D(f)=R , ну или (-∞;+∞) 2. Находим производную. Применяем формулы (2*²=4x) и x=1 (4*x=4*1=4) Итак: f '(x)=4x-4 3. Приравниваем полученную производную к нулю. f '(x)=0, 4x-4=0, решаем уравнение. 4x=4 x=1 ---⁻---(1)---⁺--- проверка знаков: проверим (+). Подставляем в полученную производную, например, цифру 2 вместо x: 4*2-4=4, число положительное, значит ставим знак плюс. Проверим (-). Подставим -1, -4-4=-8, число отрицательное, значит в интервале минус. Когда минус переходит на плюс, это считается точкой минимума. Наоборот - максимума. У нас минимум. xmin=1
Для того чтобы решать такие уравнения, сначала необходимо найти ОДЗ (область допустимым значений), или те корни, которые обращают знаменатель дроби в нуль. ОДЗ: Дальше, чтобы избавиться от знаменателя, нужно привести дроби к общему знаменателю и умножить на него обе части уравнения: Меняем знак второй дроби, чтобы у нас получилась формула сокращенного умножения, а вследствие и общий знаменатель, и умножаем на него. Решив его по т. Виета путем подбора, получим корни Возвращаемся к ОДЗ и видим, что 2 - посторонний корень, поэтому исключаем его и записываем в ответ -5. ответ: -5
(2*²=4x) и x=1 (4*x=4*1=4)
ответ: 8) n=4 или n=5
Объяснение:
дробь правильная, если числитель меньше знаменателя...
n²-n+15 < 7n+3
n²-8n+12 < 0 корни по т.Виета (2) и (6);
решение "между корнями": n ∈ (2; 6),
т.е. n∈N (по условию) может быть равно: {3; 4; 5}
остальное (сократима ли дробь) проще посчитать...
n=3: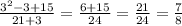
дробь сократима...
n=4: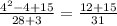
дробь НЕсократима (31-простое число))
n=5: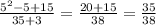
дробь НЕсократима...
решение задачи 9) на рисунке...
таких окружностей две...
касание может быть как внутренним, так и внешним...
точки касания окружностей лежат на линии центров...