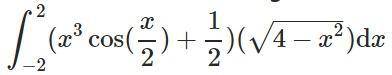
120, 135, 180, 210, 240, 315, 345, 360, 390, 420,
435, 480, 630, 675, 765, 795, 810, 840, 930, 975.
Объяснение:
Задание:
Найди трёхзначное число, кратное 15, сумма квадратов цифр которого делится нацело на 5, и все цифры которого различны.
Трехзначное число можно записать так: 100a + 10b + c.
Если оно кратно 15, то оно делится на 3 и на 5.
Это значит, что его сумма цифр делится на 3 и с = 0 или c = 5.
Кроме того, сумма квадратов цифр должна делиться на 5.
И все цифры числа должны быть различны.
Запишем систему, всего возможно два варианта:
1) c = 0 и 2) c = 5
{ a + b + c = 3n
{ a^2 + b^2 + c^2 = 5k
Напишем таблицу квадратов однозначных чисел:
0 - 0, 1 - 1, 2 - 4, 3 - 9, 4 - 16, 5 - 25, 6 - 36, 7 - 49, 8 - 64, 9 - 81.
Если сумма квадратов кратна 5, то могут быть такие варианты:
1^2 + 2^2 + 0^2 = 5 - это числа 120 и 210, кратны 15. ЭТО РЕШЕНИЯ.
1^2 + 2^2 + 5^2 = 30 - это числа 125 и 215, но они не кратны 15.
1^2 + 3^2 + 0^2 = 10 - это числа 130 и 310, они не кратны 15.
1^2 + 3^2 + 5^2 = 35 - это числа 135 и 315. ЭТО РЕШЕНИЯ.
1^2 + 8^2 + 0^2 = 65 - это числа 180 и 810. ЭТО РЕШЕНИЯ.
1^2 + 8^2 + 5^2 = 90 - это числа 185 и 815, они не кратны 15.
2^2 + 4^2 + 0^2 = 20 - это числа 240 и 420. ЭТО РЕШЕНИЯ.
2^2 + 4^2 + 5^2 = 45 - это числа 245 и 425, они не кратны 15.
2^2 + 6^2 + 0^2 = 40 - это числа 260 и 620, они не кратны 15.
2^2 + 6^2 + 5^2 = 65 - это числа 265 и 625, они не кратны 15.
3^2 + 4^2 + 0^2 = 25 - это числа 340 и 430, они не кратны 15.
3^2 + 4^2 + 5^2 = 50 - это числа 345 и 435. ЭТО РЕШЕНИЯ.
3^2 + 6^2 + 0^2 = 40 - это числа 360 и 630. ЭТО РЕШЕНИЯ.
3^2 + 6^2 + 5^2 = 65 - это числа 365 и 635, они не кратны 15.
3^2 + 9^2 + 0^2 = 90 - это числа 390 и 930. ЭТО РЕШЕНИЯ.
3^2 + 9^2 + 5^2 = 115 - это числа 395 и 935, они не кратны 15.
4^2 + 8^2 + 0^2 = 80 - это числа 480 и 840. ЭТО РЕШЕНИЯ.
4^2 + 8^2 + 5^2 = 105 - это числа 845 и 845, они не кратны 15.
6^2 + 7^2 + 0^2 = 85 - это числа 670 и 760, они не кратны 15.
6^2 + 7^2 + 5^2 = 110 - это числа 675 и 765. ЭТО РЕШЕНИЯ.
6^2 + 8^2 + 0^2 = 100 - это числа 680 и 860, они не кратны 15.
6^2 + 8^2 + 5^2 = 125 - это числа 685 и 865, они не кратны 15.
7^2 + 9^2 + 0^2 = 130 - это числа 790 и 970, они не кратны 15.
7^2 + 9^2 + 5^2 = 155 - это числа 795 и 975. ЭТО РЕШЕНИЯ.
8^2 + 9^2 + 0^2 = 145 - это числа 890 и 980, они не кратны 15.
8^2 + 9^2 + 5^2 = 170 - это числа 895 и 985, они не кратны 15.
Больше таких чисел нет.
Всего монет: 26=24(достоинством 1 руб.)+2(достоинством 2 руб.)
Взяли: 13 монет
Найти: вероятность того, что взята ровно 1 монета, достинств. 2 руб.
Если предположить, что взята ровно 1 монета достоинством 2 руб,. значит, вместе с ней, взято ровно 12 монет, дост. 1 руб.: 13-1=12
Общее число исходов - это число взять любые 13 монет из 26-и: С¹³₂₆
Число благоприятных исходов для ровно 1 монеты, дост. 2 руб.:
С¹₂ - одна и 2-х
Число благоприятных исходов для 12₂₄-и монет, дост. 1 руб.:
С¹²₂₄ - 12 из 24-х.
Используем правило произведения (если каждый объект можно выбрать из совокупности объектов, то число выбора перемножается):
С¹₂*С¹²₂₄ - число благоприятных исходов
Вероятность события(благоприятного исхода) - это отношение числа благоприятных исходов к общему числу исходов.
Составляем пропорцию:
С¹₂*С¹²₂₄/С¹³₂₆=
2!/1!(2-1)! * 24!/12!(24-12)! / 26!/13!(26-13)!=
2!/1!(2-1)!=2*1/1*1=2
24!/12!(24-12)!=13*14*15*16*...*24/1*2*3*4*...*12)=2704156
26!/13!(26-13)!=14*15*16*17*...*26/1*2*3*4...*13)=10400600
2*2704156/10400600=0.52
ответ: Найдите вероятность того, что среди выбранных монет ровно одна монета достоинством 2 руб. = 0.52
Так как интеграл с корнем- есть полуокружность с радиусом два,то площадь круга = pi r^2 = 4pi ,площадь полукруга 1/2 * 4pi. Перед интегралом стоит 1/2,следовательно 4pi/4=pi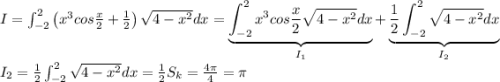
Заметим,что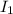
- нечётная функция,следовательно, 