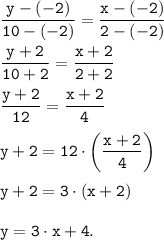
1) 8х + 1,3 = 34,9 - 8х 2) -4 = -2/8х
8х + 8х = 34,9 - 1,3 х = -4 : (-2/8)
16х = 33,6 х = 4 · 8/2
х = 33,6 : 16 х = 2 · 8
х = 2,1 х = 16
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
3) 9х = 108 4) 6х - 8 = 6,4
х = 108 : 9 6х = 6,4 + 8
х = 12 6х = 14,4
х = 2,4
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
5) 4(х - 2) = -1 6) 40х = -32
4х - 8 = -1 х = -32 : 40
4х = 8 - 1 х = -0,8
4х = 7
х = 7/4
х = 1 целая 3/4 = 1,75 (в десятичных дробях)
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
7) 4х - 2 = 22 8) 5х - 13 + 2(3 - х) = -х + 16
4х = 22 + 2 5х - 13 + 6 - 2х = -х + 16
4х = 24 5х - 2х + х = 16 - 6 + 13
х = 24 : 4 4х = 23
х = 6 х = 23/4 = 5 целых 3/4 = 5,75
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
9) 4(3х + 5) - 3(4х - 1) = 22х + 12
12х + 20 - 12х + 3 = 22х + 12
12х - 12х - 22х = 12 - 3 - 20
-22х = -11
х = -11 : (-22)
х = 1/2 = 0,5 (в десятичных дробях)
y=3·x+4
Объяснение:
Абсцисса координат точек M(-2;-2) и N(2;10) различные (то есть прямая не проходит вертикально) и поэтому будем искать уравнение прямой в виде с угловым коэффициентом:
y=k·x+b.
Так как прямая проходить через точки M(-2;-2) и N(2;10), то подставим координаты точек в уравнение и получим систему уравнений относительно k и b:
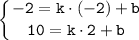
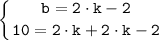
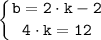
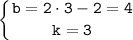
Подставляем найденные решения получим:
y=3·x+4.
Для решения задачи можно использовать общий вид уравнения прямой, проходящей через 2 точки M(x₁; y₁) и N(x₂; y₂):
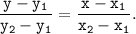
При заданных значениях координат M(-2;-2) и N(2;10) имеем: