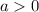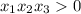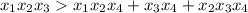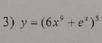
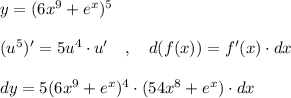
Дифференциал функции равен произведению производной этой функции на дифференциал аргумента.
dу=y'*dx
dу=(54x⁸+eˣ)*(6x⁹+eˣ)⁴*dx
здесь находили производную от сложной функции.
у=v⁵
y'=5v⁴*v'
v=(6x⁹+eˣ)
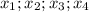
 это
это 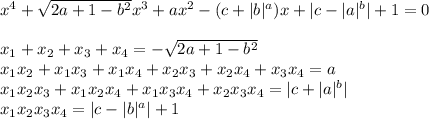
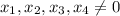
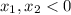 без потери общности можно взять
без потери общности можно взять 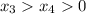
![b \in [-\sqrt{2a+1};\sqrt{2a+1} ] \\ a-\frac{1}{2}](/tpl/images/0281/2774/4e19b.png)
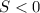 , но это не верно , так как стоит модуль , значит четыре корня не может быть.
, но это не верно , так как стоит модуль , значит четыре корня не может быть. 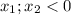 по второму условию следует что
по второму условию следует что