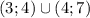
Объяснение:
Решим первое неравенство. ОДЗ:
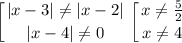
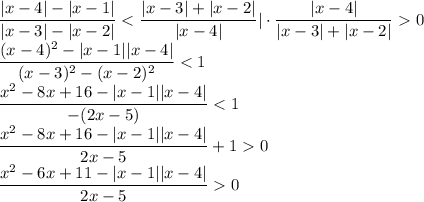
Если x < 1 или x ≥ 4, то модули раскрываются с одним знаком, произведение подмодульных выражений положительно:
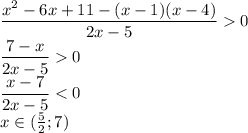
Учитывая, что x < 1 или x ≥ 4, а также учитывая ОДЗ,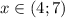 
Если 1 ≤ x < 4, то модули раскрываются с разным знаком, произведение подмодульных выражений отрицательно:
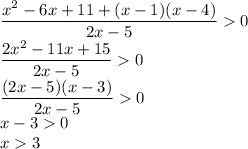
Учитывая, что 1 ≤ x < 4 и ОДЗ,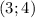 
.
Объединяя полученные промежутки, получаем, что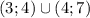
Решим второе неравенство. Пусть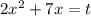 
. Тогда
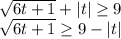
Если правая часть отрицательна, то неравенство выполняется на ОДЗ, так как квадратный корень всегда неотрицателен:
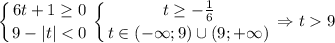
Если правая часть неотрицательна, то обе части можно возвести в квадрат:
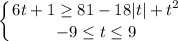
Если t ≥ 0, то модуль раскрывается с плюсом, первое неравенство имеет вид:
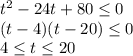
Если t < 0, то модуль раскрывается с минусом, неравенство имеет вид:
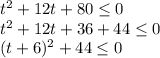
Сумма неотрицательного и положительного чисел не может быть неположительной. В данном случае решений нет.
Учитывая -9 ≤ t ≤ 9, решением данного случая является ![t\in[4;9]](/tpl/images/1358/7181/70120.png)
Объединив оба случая, получаем t ≥ 4,
![2x^2+7x-4\geq 0\\(x+4)(2x-1)\geq 0\\x\in(-\infty;-4]\cup[\frac{1}{2};+\infty)](/tpl/images/1358/7181/42d33.png)
Пересечём полученные решения: ответом будет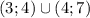
Каждая сторона вписанного треугольника соединяет середины сторон исходного и поэтому является средней линией. Средняя линия треугольника равна половине длины стороны, которой она параллельна.
Коэффициент k подобия этих треугольников ½
.Отсюда каждая сторона первого вписанного треугольника равна 8·½ =4 см
.Пусть периметр исходного треугольника будет Р₁,
периметр первого вписанного треугольника- р₂
Тогда Р₁=8·24 см
р₂=24·½ =12 cм
Отношение периметров подобных треугольников равно коэффициенту их подобия.
р₃=12·½=6 см
р₄=6·½=3 см
р₅=3·½=1,5 см
р₆=1,5·½=0,75 см
р₇=0,75·½=0,375 см
р₈=0,375·½=0,1875 см
Как Вы, наверное, обратили внимание, последовательность периметров сторон вписанных треугольников - геометрическая прогрессия, где каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же число ½.
Каждый член геометрической прогрессии {bn} определяется формулой
bn = b₁ · qⁿ⁻¹
b₈=24·(½)⁷=0,1875 см