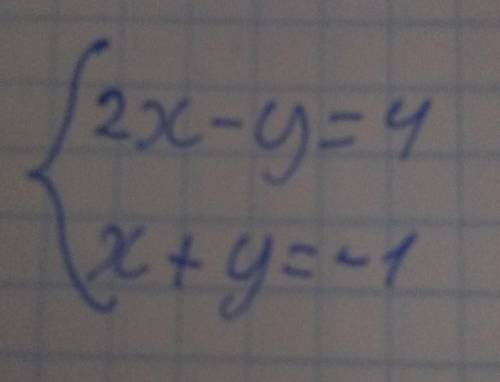
Решение системы уравнений (1; -2).
Объяснение:
Решить систему уравнений:
2х-у=4
х+у= -1
Выразить х через у во втором уравнении, подставить выражение в первое уравнение и вычислить у:
х= -1-у
2(-1-у)-у=4
-2-2у-у=4
-3у=4+2
-3у=6
у=6/-3
у= -2;
х= -1-(-2)
х= -1+2
х=1
Решение системы уравнений (1; -2).

Обозначим cлагаемые за Х,У,Z
(X+Y+Z)/3>=1
Согласно неравенству о среднем арифметическом и среднем геометрическом достаточно доказать :
ХУZ>=1
Вернемся к исходным обозначениям
8abc>=(a+b)(b+c)(a+c)
Снова согласно неравенству о среднем арифметическом и среднем геометрическом видим
a+b>=2sqrt(ab) b+c>=2sqrt(сb) (a+c)>=2sqrt(ac)
поэтому можим заменить сомножители справа на произведение
2sqrt(ab)*2sqrt(aс)*2sqrt(сb)=8abc, что и доказывает неравенство.
Равенство достигается только при а=с=b
ответ : (1; - 2)
Решение прилагаю