
Сечением куба может быть любая из указанных в условии фигур. В приложении рисунки возможных сечений. Доказательство основывается на свойствах куба : все рёбра равны, все грани являются равными квадратами, грани попарно параллельны.
1) Произвольный треугольник получится в сечении, если от одной вершины куба отложить по трём рёбрам отрезки разного размера. Треугольник в сечении будет образован гипотенузами прямоугольных треугольников разной длины.
2) Например, правильный треугольник получится в сечении, если его сторонами будут диагонали смежных граней. Так как все грани куба равны, то диагонали граней тоже равны, то есть треугольник равносторонний.
3) Например, прямоугольник можно получить в сечении, если построить его на диагоналях противоположных граней. Двумя другими сторонами прямоугольника будут рёбра куба.
4) Например, квадрат получится в сечении, параллельном любой из граней куба.
5) Например, трапеция получится в сечении, если "наклонить" диагональное сечение. В нижней грани сечение пройдёт по диагонали, а в верхней грани по отрезку, параллельному диагонали грани.
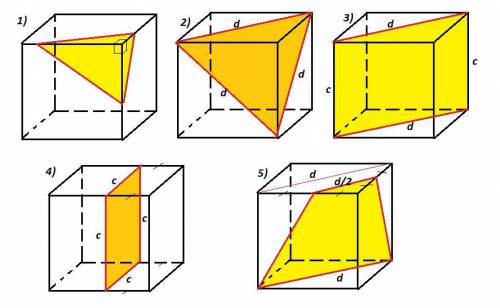
График линейной функции (нет квадратных одночленов) - прямая. Строят прямую по двум точкам. Выберем значения x, найдём соответствующие значения y ⇒ получим точки. Выбирать значения x лучше так, чтобы получить целые координаты точек.
x₁ = -2 ⇒ y₁ = 1,8 - 0,6 × (-2) = 3 ⇒ точка (-2; 3);
x₂ = 3 ⇒ y₂ = 1,8 - 0,6 × 3 = 0 ⇒ точка (3; 0).
Получили две точки. Отмечаем их на координатной плоскости, соединяем линией. Получили нужный график (см. приложение).
Определить принадлежность точек графику данной функции.Чтобы проверить, принадлежит ли точка функции, нужно подставить её координаты в уравнение функции. Если получается верное равенство - точка принадлежит графику функции.
1) А (-2; 5) ⇒ 1,8 - 0,6 × (-2) = 1,8 + 1,2 = 3 ≠ 5 ⇒ точка А не принадлежит.
2) B (-5; 4,8) ⇒ 1,8 - 0,6 × (-5) = 1,8 + 3 = 4,8 ⇒ точка B принадлежит.
ответ: A не принадлежит, B принадлежит.