Решение.
Впишем четырехугольник ABCD в прямоугольник EFGH со сторонами,
параллельными диагоналям (EF || AC и EH || BD) - смотри рисунок.
Пусть L - точка пересечения прямых DC и EF, а M - точка на прямой HG такая, что LM || FG.
Тогда ABLC - параллелограмм, следовательно, AB = CL.
Так как GM = FL = EB = HD и AH = CG, то треуг-к AHD = треуг-ку CGM ,
следовательно, AD = CM. BC + CM = BC + AD .
Но BM = DL как диагонали прямоугольника BLDM, и DL = DC + CL = DC + AB.
Следовательно, AD + BC = DL = DC + CL = DC + AB, что и требовалось доказать.
2*3^n≤2^n+4^n
преобразуем
2 ≤ (2^n+4^n ) / 3^n = (2/3)^n +(4/ 3)^n
в правой части оба слагаемые положительные числа
первое слагаемое (2/3)^n - дробь -всегда меньше 1
второе слагаемое (4/3)^n - дробь -всегда больше 1
достаточное условие доказательства , чтобы одно из слагаемых было БОЛЬШЕ 2
рассмотрим n=1,2,3
n=1
(2/3)^1 +(4/ 3)^1 = 2/3+4/3=6/3 =2 <выполняется равенство 4/3 < 2
n=2
(2/3)^2 +(4/ 3)^2 = 4/9+16/9=20/9 =2+2/9 >2 <выполняется НЕравенство 16/9 < 2
n=3
(2/3)^3 +(4/ 3)^3 = 8/27+64/27=72/27 =2+18/27 <выполняется НЕравенство 64/27 > 2
второе слагаемое (4/3)^n > 2 , для всех 3 ≤ n
следовательно, для любого натурального n справедливо заданное неравенство
ДОКАЗАНО
1) - 112
2) 87
3) - 13
Объяснение:
1) 6* (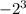
) - 4 * 
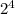= 6 * (-8) - 4 * 16 = - 48 - 64 = - 112
2) 2 * 3 + (6 *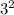
- (
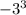)) = 6 + (6 * 9 + 27) = 6 + 54 + 27 = 87
3)
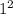- 2 * (
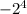) + 6 * 3 = 1 - 2 * 16 + 6 * 3 = 1 - 32 + 18 = - 13