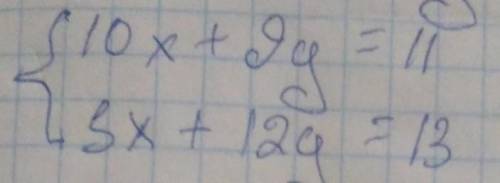
В решении.
Объяснение:
Решить систему уравнений.
а подстановки:
10х+9у=11
5х+12у=13
Разделить первое уравнение на 10 для упрощения:
х+0,9у=1,1
5х+12у=13
Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:
х=1,1-0,9у
5(1,1-0,9у)+12у=13
5,5-4,5у+12у=13
7,5у=13-5,5
7,5у=7,5
у=7,5/7,5
у=1;
х=1,1-0,9у
х=1,1-0,9*1
х=0,2.
Решение системы уравнений (0,2; 1).
б сложения:
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, чтобы коэффициенты при неизвестном каком-то были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают уравнения, можно умножать обе части уравнения на одно и то же число, делить.
В данной системе нужно второе уравнение умножить на -2:
10х+9у=11
-10х-24у= -26
Складываем уравнения:
10х-10х+9у-24у=11-26
-15у= -15
у= -15/-15
у=1;
Теперь подставить значение у в любое из двух уравнений системы и вычислить х:
10х+9у=11
10х=11-9*1
10х=2
х=0,2
Решение системы уравнений (0,2; 1).
в)графически:
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Прежде преобразуем уравнения в более удобный для вычислений вид:
10х+9у=11 5х+12у=13
9у=11-10х 12у=13-5х
у=(11-10х)/9 у=(13-5х)/12
Таблицы:
х -1 0 1 х -1 2 5
у 2,3 1,2 0,1 у 1,5 0,25 -1
Координаты точки пересечения графиков функций (0,2; 1).
Решение системы уравнений (0,2; 1).
При имеющихся исходных данным возможно 2 ответа:
1) b₁ = 6; q = 1/4;
1) b₁ = -6; q = -1/4;
Объяснение:
Член геометрической прогрессии с номером n вычисляется по формуле
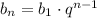
b₄ - b₂ = b₁ · q³ - b₁· q = b₁q(q² - 1)
b₆ - b₄ = b₁ · q⁵ - b₁· q³ = b₁q³(q² - 1)
По условию
b₁q(q² - 1) = -45/32 (1)
b₁q³(q² - 1) = -45/512 (2)
Преобразуем выражение (2)
b₁q³(q² - 1) = b₁q(q² - 1) · q²
В численном виде это можно записать как
-45/512 = -45/32 · q²
Откуда
q² = -45/512 : (-45/32)
q² = 1/16
q = ±1/4
Подставим q = 1/4 в выражение (1)
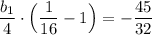
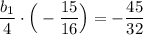
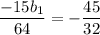
0.5b₁ = 3
b₁ = 6
Подставим q = -1/4 в выражение (1)
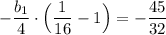
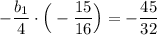

0.5b₁ = -3
b₁ = -6
Проверка:
1) b₁ = 6; q = 1/4
b₂ = 6 · 1/4 = 3/2
b₄ = 6 · 1/64 = 3/32
b₄ - b₂ = 3/32 - 3/2 = -45/32
b₆ = 6 · 1/1024 = 3/512
b₆ - b₄ = 3/512 - 3/32 = -45/512
2) b₁ = -6; q = -1/4
b₂ = -6 · (-1/4) = 3/2
b₄ = -6 · (-1/64) = 3/32
b₄ - b₂ = 3/32 - 3/2 = -45/32
b₆ = -6 · (-1/1024) = 3/512
b₆ - b₄ = 3/512 - 3/32 = -45/512
...............................