функция не определена в 2х точках, это корни квадратного уравнения, находящегося в знаменателе. Его корни x=1 и x=-3. Это и есть точки разрыва функции.
1) x=1 для определения рода разрыва воспользуемся теорией пределов.
предел при x стремящемуся к 1му со стороны минуса
lim=5x/x^2+2x-3=5x/x*(x+2-3/x)=5/(x+2-3/x)=-беск.
предел при х стремящемуся к 1 со стороны плюса
lim=+беск. Рассчеты те же, только с другой стороны приближаемся к этой точке.
2) x=-3
предел при х стремящемуся к -3 со стороны минуса
lim=-беск
предел при х стремящемуся к -3 со стороны плюса
lim=беск.
Во втором пункте рассуждения такие же, только точка другая
Глядя на то что пределы в каждой из точек бесконечны убеждаемся в том что точки разрыва х=1 и х=-3 являются точками разрыва 2го рода.
Если есть вопросы по теотрии то в личку отвечу.
Обозначим х -длину одной стороны, у- длину второй стороны. При это х и у > или равны 0
На основании этого составим систему неравенств:
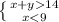
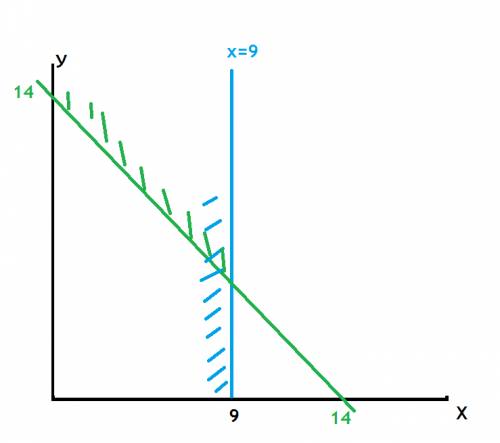
Теперь решим, графически (см. вложение)
Первое уравение рассмотрим как равенство, получим: х+у=14, т.е у=14-х.
Там где на рисунке есть штриховка и синяя и зеленая и лежат наши решения. Значит чтобы найти пределы в которых может изменяться y, нужно найти точку пересечения прямых у=14-х и х=9. Это делается просто в 1 уравение подставляем х=9 и получаем, у=5.
Значит получаем следующее решение (поскольку у нас стороны положительные, то мы рассматриваем только положительную четверть координат).
И значит решение будет: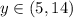 
ответ: 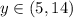, где у это сторона прямоугольника
привет всем брат я не знаю