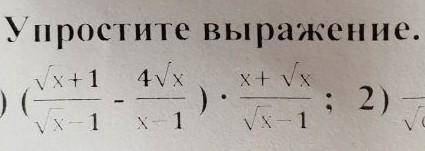
2. Исследуем функцию на монотонность и на экстремум:
Критические точки функции:
,
,
Определим знак производной в каждом интервале монотонности:
, точка max, так как производная изменила знак с "+" на "−",
, точка min, так как производная изменила знак с "−" на "+".
Вычислим сам экстремум функции в этих точках:
3. Исследуем функцию на выпуклость, вогнутость кривой и перегиб:
Критические точки: , , ,
Определим знак II производной в интервале кривизны:
, значит, кривая выпуклая на промежутке,
, значит, кривая вогнутая на промежутке;
Вычислим ординату точки перегиба:
4. Найдём дополнительные точки графика:
По результатам исследования строим график функции:
Пример 2. Исследовать функцию по первой и второй производной и построить её график: .
1. Область определения функции ,
точка разрыва, чтобы определить её характер, найдём правосторонний и левосторонний пределы функции в этой точке:
Значит, точка разрыва рода,
прямая вертикальная асимптота графика функции.
Найдём наклонную асимптоту графика:
где угловой коэффициент прямой найдём по формуле
Так как существует, то есть и наклонная асимптота. Вычисляем коэффициент b:
Значит, наклонная асимптота графика имеет уравнение .
2. Исследуем функцию на монотонность и на экстремум:
, учтем правило дифференцирования
Критические точки функции:
, , , , х=2,
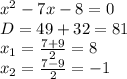
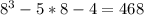- не подходит
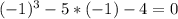- подходит
Объяснение:
********************************************