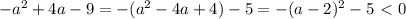
Дробь не имеет смысла если её знаменатель равен нулю т.к. на ноль делить нельзя.
\dfrac{x}{x-4} ;\; x-4=0;\; \bold{x=4} dfrac{2b^2-9}{b(b-5)} ;\; b(b-5)=0;\; \bold{b=\{0;5\}}.
Дробь равна нулю если числитель равен нулю, а знаменатель - не равен.
\dfrac{x+1}{x} =0;\; \begin{Bmatrix}x+1=0\\x\ne 0\end{matrix} \\\begin{Bmatrix}x=-1\\x\ne 0\end{matrix} \qquad \bold{x=-1}dfrac{x(x-2)^2 }{x-2} =0;\; \begin{Bmatrix}x(x-2)^2 =0\\x-2\ne 0\end{matrix} \\\begin{Bmatrix}x=\{0;2\}\\x\ne 2\end{matrix} \qquad \bold{x=0}.
Объяснение:
удачи получить хорошую отметку
Дробь не имеет смысла если её знаменатель равен нулю т.к. на ноль делить нельзя.
\dfrac{x}{x-4} ;\; x-4=0;\; \bold{x=4} dfrac{2b^2-9}{b(b-5)} ;\; b(b-5)=0;\; \bold{b=\{0;5\}}.
Дробь равна нулю если числитель равен нулю, а знаменатель - не равен.
\dfrac{x+1}{x} =0;\; \begin{Bmatrix}x+1=0\\x\ne 0\end{matrix} \\\begin{Bmatrix}x=-1\\x\ne 0\end{matrix} \qquad \bold{x=-1}dfrac{x(x-2)^2 }{x-2} =0;\; \begin{Bmatrix}x(x-2)^2 =0\\x-2\ne 0\end{matrix} \\\begin{Bmatrix}x=\{0;2\}\\x\ne 2\end{matrix} \qquad \bold{x=0}.
Объяснение:
удачи получить хорошую отметку
(a заменил на x для удобства)
Вершина у параболы находится по формуле
Коэффициент а (ax^2+bx+c) в нашей формуле отрицательный, следовательно ветви направлены вниз
В итоге получаем что вершина параболы ниже оси Оx, а ветви направлены вниз, из чего делаем вывод, что парабола будет принимать только отрицательные значения