Пусть х часов требуется мастеру на выполнение всего заказа, время, которое затрачивает на эту работу ученик равно (х+16) часов. 1/х - часть заказа, которую выполняет мастер за 1 час, 6/х - часть заказа, выполняемая мастером за 6 часов. 1/(х+16) - часть заказа, которую выполняет ученик за 1 час, за 8 часов работы ученик выполнит 8/(х+16), что меньше работы, выполненной мастером на
(6/х-8/(х+16)) или 1/20 заказа. Составим и решим уравнение:
6/х-8/(х+16)=1/20 |*20x(х+16)
120(х+16)-160х=х(х+16)
120х+1920-160х=х^2+16x
x^2+16x+40x-1920=0
x^2+56x-1920=0
x^2-24x+80x-1920=0
x(x-24)+80(x-24)=0
(х-24)(х+80)=0
х-24=0 х+80=0
х1=24 х2=-80 (время работы не может быть отрицательным числом)
х+16=24+16=40
1:24=1/24 заказа - выполняет мастер за 1 час
1:40=1/40 заказа - выполняет ученик за 1 час
1/24+1/40=5\120+3/120=8/120=1/15 заказа - выполняют мастер и ученик за 1 час, работая вместе
1:1/15=15 (ч.)
ответ: при совместной работе мастер и ученик выполнят заказ за 15 часов.
а - длина прямоугольника
b - ширина прямоугольника
=================================================================
Р=28 м
S=40 м²
а - ? м
b - ? м
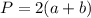 (1)
(1)
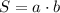 (2)
(2)
из формулы площади прямоугольника (2) выводим формулу нахождения ширины
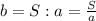
подставляем в формулу периметра прямоугольника (1)
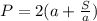
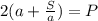
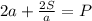
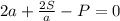 /·a
/·a
умножаем на а для того, чтобы избавится от знаменателя
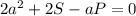
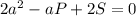
подставим в уравнение данные P и S
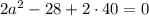
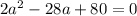
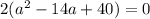
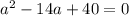
Квадратное уравнение имеет вид:
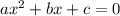
Cчитаем дискриминант:
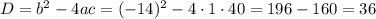
Дискриминант положительный
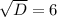
Уравнение имеет два различных корня:
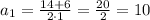
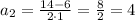
Следовательно стороны равны 10м и 4м соответственно
ответ: 10м и 4м стороны прямоугольника.
Проверка:
Р=2(а+b)=2(10+4)=2·14=28 (м)
S=a·b=10·4=40 (м²)
Объяснение:
f(x)=-2x² M(-1:0)
f(-1)=-2
f'(x)=-4x
f'(-1)=4
y=-2+4(x+1)=-2+4x+4=4x+2
y=4x+2