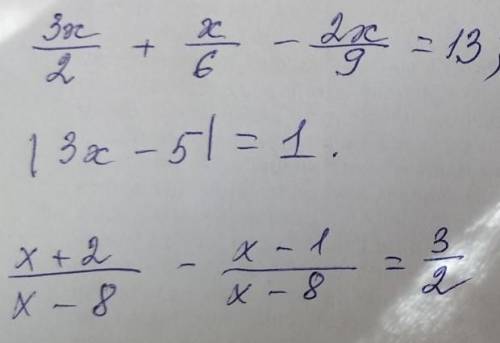
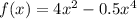
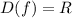
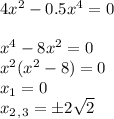
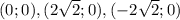 - точки пересечения с осью Ох
- точки пересечения с осью Ох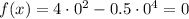
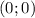 - точки пересечения с осью Оу
- точки пересечения с осью Оу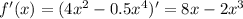
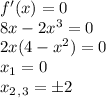
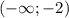 и
и 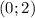 , а убывает -
, а убывает - 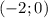 и
и 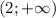 . В точке
. В точке  функция имеем локальный максимум, а в точке
функция имеем локальный максимум, а в точке 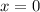 - локальный минимум
- локальный минимум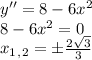
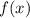 называется четной, если
называется четной, если 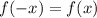
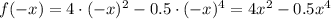
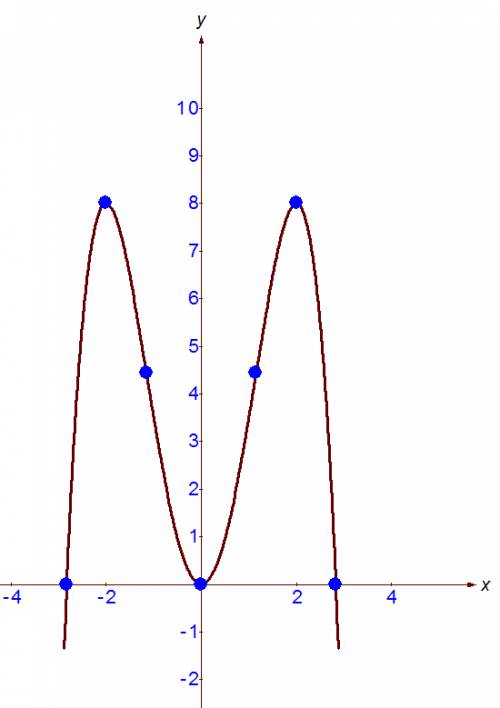
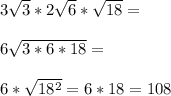
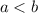

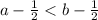 -верно
-верно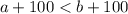 -верно
-верно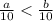 - верно
- верно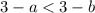 равносильно
равносильно 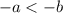 (при умножении обеих частей на одинаковый множитель знак неравенства меняется на противоположный)
(при умножении обеих частей на одинаковый множитель знак неравенства меняется на противоположный)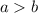
на фото................