х - у = 8
х + у = - 3
Выразим у из каждого уравнения:
у = х - 8
у = - х - 3
Построим графики двух этих функций. Это линейные функции, графиком являются прямые. Для построения каждой прямой надо знать две точки.
у = х – 8
х1 = 0 х2 = 1
у1 = -8 у2 = -7
(0; -8) (1; -7)
у = - х - 3
х1 = 0 х2 = 1
у1 = - 3 у2 = -4
(0; -3) (1; -4)
По данным точкам строим две прямые. Находим точку пересечения. Координаты точки пересечения будут ответом в данной системе.
х = 2,5
у = -5,5
Чертёж прилагается.
ответ: (2,5; -5,5)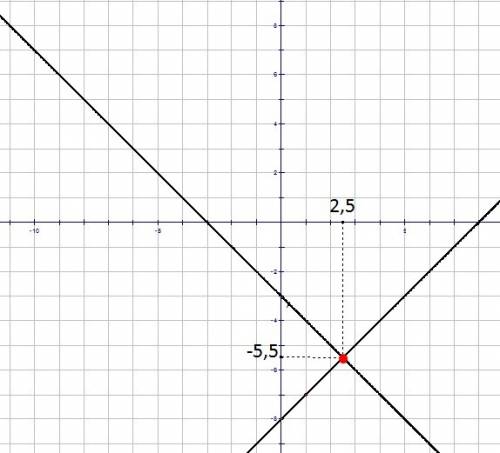
Решение системы уравнений (-2; -1); (2; 1).
Объяснение:
Решите алгебраического сложения систему уравнений:
2х² + у² = 9
у² - х² + 3 = 0
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, чтобы коэффициенты при неизвестном каком-то были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают уравнения, можно умножать обе части уравнения на одно и то же число, делить.
В данной системе нужно второе уравнение умножить на 2:
2х² + у² = 9
2у² - 2х² = -6
Складываем уравнения:
2х² - 2х² + у² + 2у² = 9 - 6
3у² = 3
у² = 1
у=±√1
у=±1;
Теперь подставить значение у в любое из двух уравнений системы и вычислить х:
2х² + у² = 9
2х² = 9 - у²
2х² = 9 - 1
2х² = 8
х² = 4
х = ±√4
х=±2
Решение системы уравнений (-2; -1); (2; 1).