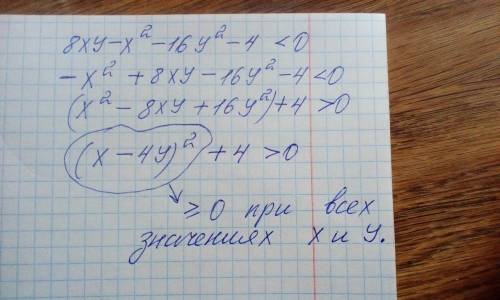
Ну короче смотри: узнать надо первоначальную скорость, значит её возьмём за Х.
Значит обратная скорость = х+12.
Время (t) на первоначальное направление = 300:Х.
Время (t) на обратное направление = 300:(Х+12)
Известно, что на обратный путь он затратил на 50 мин меньше. Это зацепка к решению задачи. Переведём 50 мин в дробь (1 час=60 минут, т.е. 6/6. значит 50 мин будет 5/6). Теперь сделаем уравнение, полузуясь этой зацепкой. (я так много задач решил))).
300:Х-300:(Х+12)=5\6.
6(300(Х+12)-300Х)=5Х(Х+12) . <-- как я это сделал объянять долго)))
5Х^2+60X=6*300*12. Итак, Х справа для лёгкости сократим на 5. Слева посчитаем:
Х^2+12X-4320=0
X=(-12+132):2=60
X=60. Задача решена)
≈ 24,6°
Объяснение:
Для начала найдем вектор по координатам точек:
AB = {Bx - Ax; By - Ay; Bz - Az}
AB = {3 - 3; -2 - (-1); 2 - (-3)}
AB = {0; -1; 5}
CD = {Dx - Cx; Dy - Cy; Dz - Cz}
CD = {1 - 2; 2 - (-2); 2 - 3}
CD = {-1; 4; -1}
Теперь найдем скалярное произведение векторов:
AB · CD = ABx · CDx + ABy · CDy + ABz · CDz
AB · CD = 0 · (-1) + (-1) · 4 + 5 · (-1)
AB · CD = 0 - 4 - 5
AB · CD = -9
Затем найдем длины векторов:
|AB| =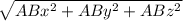 
|AB| =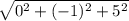 
|AB| =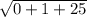 
|AB| =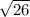 
|CD| =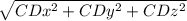 
|CD| =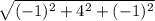 
|CD| =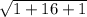 
|CD| =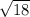 
|CD| = 3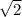
Найдем косинус угла между векторами:
cos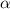 
= 
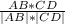
cos =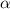 
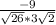
cos =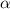 
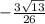
cos 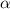= ≈ -0.41602514716892186
И наконец-то находим по таблице брадисса угол, с найденого косинуса
Это ≈ 24,6°
