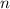1) вершина в точке О(0; 0) 2) ветви параболы направены вниз 3) заполняем таблицу: х= 1 -1 2 -2 1/3 -1/3 у=-3 3 -12 -12 -1/3 -1/3
Чертим систему координат, отмечаем положительное направление стрелками вправо и вверх, подписываем оси вправо - ось х, вверх - ось у, отмечаем начало координат - точку О(0; 0) Далее выбираем единичный отрезок, равный 1 клетке.
Ставим точки из таблицы и отмечаем точку О(0;0), через точки проводим плавную линию, подписываем график у=-3х² . Всё!
1) Это верно даже для 3-х чисел...)) Из 3-х любых целых чисел всегда можно выбрать 2 таких, что они будут либо оба четные, либо оба нечетные. То есть 2 числа, допустим, четное и нечетное. Третье будет либо четным, либо нечетным. Поэтому среди 3-х любых целых чисел всегда можно найти пару четных или пару нечетных чисел.
Для чего нам это нужно? - С четными все понятно: 2n - первое число, 2(n+k) - второе. Тогда: 2n + 2(n+k) = 2*(n+n+k) = 2*(2n+k) Результатом умножения на 2 любого целого числа будет четное число.
Теперь рассмотрим 2 нечетных числа: 2n+1 - первое число, 2(n+k)+1 -второе число Сумма: 2n+1 + 2(n+k)+1 = 2*(2n+k)+2 - очевидно, также четное.
Таким образом, из 2016 целых чисел всегда можно выбрать 2 числа так, чтобы их сумма была четной.
2) Нет, нельзя. Если такое разбиение есть, то полная сумма 1 + 2 + ... + 21 разбивается на две равные части: 1. сумма всех максимальных чисел в каждой группе и 2. сумма всех остальных по всем группам.
Поскольку полная сумма 1 + 2 + ... + 21 = ((1+21) * 21):2 = 11 * 21 = 231 нечётна, то это невозможно.
Учитывая, что cумма квадратов трех чисел неотрицательна, то для ЛЮБЫХ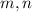
cправедливо неравенство:
Равенство наступает при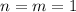
.
Как видим, неравенство верно при ВСЕХ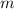
и 