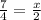2) 7Х=Х+25 3) 3Х+16=9-10Х
1) 12⁻³=1/12³=1/1728
2) 3⁻⁴=1/3⁴=1/81
3) (-2)⁻⁶=1/(-2)⁶=1/64
4) (-5)⁻³=-1/5³=-1/125
5) 100⁻¹=1/100=0,01
6) (-1/8)⁻¹=-8
7) (2/3)⁻³=(3/2)³=27/8=3 3/8
8) (-7/9)⁻²=(9/7)²=81/49=1 32/49
9) (1 2/3)⁻¹=(5/3)⁻¹=3/5=0,6
10) (-1 1/4)⁻³=(-5/4)⁻³=(-4/5)³=-64/125
11) (0,01)⁻³=(1/100)⁻³=100³=1 000 000
12) (1,6)⁻²=(1 3/5)⁻²=(8/5)⁻²=(5/8)²=25/64
1) 3⁻³ + 6⁻² = 1/27 + 1/36 = 4/108 + 3/108 = 7/108
2) (2/3)⁻¹ + (-1,7)⁰ - 2⁻³ = 3/2 + 1 - 1/8 = 12/8 + 1 - 1/8 = 11/8 + 8/8 = 19/8 = 2 3/8
3) (3/4)⁻² * 2⁻³ = 16/9 * 1/8 = 16/(9*8) = 2/9
4) 10⁻¹ + 5⁻² - 2⁻³ = 1/10 + 1/25 - 1/8 = 20/200 + 8/200 - 25/200 = 3/200 = 15/1000 = 0,015
Число a должна иметь вид : a =36k +18 .
Т.к. число a трехзначное, то 100<36k+18 <1000 ⇔3 ≤ k ≤ 27.
Количество таких чисел: n=27-(3-1) = 25 .
a∈{ 126 ; 162 , 198 ; ...972} * * * Составляют арифметическую прогрессию * * *
* ! 702 = 126 +(n-1)36⇒n=17 * * *
702 =36k+18 при k =19.
* * * P.S. * * *
a = 9x = 4y +2 ; || 100 <9x <1000⇔12 <x ≤111 ||
y =(9x -2)/4 ;
y = 2x + (x-2)/4 ; k= (x-2)/4⇒x=4k+2 . || y =2x+k =2(4k+2)+k =9k+4 ||
⇒ { x =4k +2 . y =9k+4 .
|| 12 ≤ 4k+2 ≤ 111⇔2,5 ≤ k ≤27,25 ; 3 ≤ k ≤ 27 ||
a =9x =36k+18.
число a =9x =9(4k +2) =36k +18.