* * * * * * * * * * * * * * * * * * * * * *
Числа x, y, z образуют (в указанном порядке) геометрическую прогрессию; числа x, y+10, z образуют (в указанном порядке) арифметическую прогрессию, а числа x, y+10 и z+80 (в указанном порядке) – также геометрическую прогрессию. Найдите x, y и z.
ответ: 5 ; 15 и 45 или 5/9 ; -25/9 и 125/9 .
Объяснение: * * * x ; x*q ,x*q² , x≠0 * * *
y =x*q ; z =x*q², где q знаменатель геометрической прогрессии
числа x, y+10, z образуют (в указанном порядке) арифметическую прогрессию , значит y+10 =(x+z)/2⇔ 2(y+10) =x+z ⇔(символ эквив)
2(x*q+10) = x+x*q²⇔ x+x*q²- 2x*q=20⇔ x*(q-1)² =20 (1)
числа x, y+10 и z+80 (в указанном порядке) – также геометрическую прогрессию,следовательно (y+10)² = x(z+80) ⇔(x*q+10)² = x(xq²+80) ⇔
x²*q²+20x*q+100 = x²q²+80x ⇔20x*q+100 =80x⇔x*q+5 =4x ⇔
x*(4-q) = 5 (2)
первое уравнение (1) разделим на уравнение (2) получаем
x*(q-1)²/ x*(4-q) =20/5 ⇔(q-1)²/ (4-q) =4 ⇔ q²-2q+1 =16 -4q
q²+2q- 1 5 =0 ⇒ q =3 ; q = - 5
a) q = 3 ⇒ x = 5/(4-q) = 5/(4-3) = 5 5 ; 15 ; 45
b) q = - 5 ⇒ x = 5/(4-q) = 5/ (4-(5)) =5/9 5/9 ; -25/9 ; 125/9
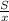
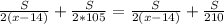
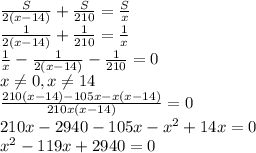
Пусть цена 1 тетради "х" коп, цена 1 карандаша "у" коп. Так как первый ученик купил 3 тетради, значит за них уплатил 3х , за 2 карандаша уплатил 2у коп. Нам известно, что за них вместе заплатил 6 р 60 коп = 660 коп, составим уравнение: 3х = 2у = 660. Второй ученик купил 2 тетради, значит уплатил 2х коп, за 2 карандаша уплатил 2у коп. За свою покупку второй ученик заплатил 4 р 60 коп = 460 коп составим уравнение: 2х + 2у = 460. Составим ситему уравнений и решим её: {3x + 2у = 660; {2x + 2у = 460. Умножим второе уравнение на ( -1), и сложим данные уравнения, для избавления от одной переменной: {3х + 2у = 660; {- 2х - 2у = - 460; (3х - 2х) + (2у -2у) = 660 - 460; х = 200. Значит, 1 тетрадь стоит 200 коп = 2 руб. Подставим значение "х" в первое уравнение: 3 * 200 + 2у = 660; 600 + 2у = 660; 2у = 660 - 600; 2у = 60; у = 60 : 2; у = 30. Значит 1 карандаш стоит 30 коп. ответ: тетрадь 2руб, карандаш 30 коп.